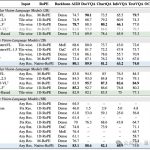
推薦幾個出論文的好方向

允中?發自 凹非寺
量子位 編輯 | 公眾號 QbitAI

加入AI行業拿到高薪僅僅是職業生涯的開始。現階段AI人才結構在不斷升級，對AI人才的要求也不斷升高，如果對自己沒有很高的要求，其實很容易被快速發展的趨勢所淘汰。

為了迎合時代的需求，貪心科技推出了《機器學習高端訓練營》。這個訓練營的目的很簡單：想培養更多高端的人才，幫助那些即將或者目前從事科研或已從事AI行業的朋友提高技術深度。

本期已經是我們開設的第5期，我們對課程內容做了大幅度的更新，一方面新增了對前沿主題的講解如圖神經網絡（GCN，GAT等），另外一方面對核心部分（如凸優化、強化學習）加大了對理論層面上的深度。除此之外，也會包含科研方法論、元學習、解釋性、Fair learning等系列主題。目前在全網上應該找不到類似體系化的課程。課程仍然采用全程直播授課模式。

那什么樣的人適合來參加高階班呢？

• 從事AI行業多年，但技術上感覺不夠深入，遇到了瓶頸；
• 停留在使用模型/工具上，很難基于業務場景來提出新的模型；
• 對于機器學習背后的優化理論、前沿的技術不夠深入；
• 計劃從事尖端的科研、研究工作、申請AI領域研究生、博士生；
• 打算進入頂尖的AI公司如Google，Facebook，Amazon， 阿里等；
• 讀ICML，IJCAI等會議文章比較吃力，似懂非懂，無法把每個細節理解透；

01 課程大綱

第一部分：凸優化與機器學習

第一周：凸優化介紹

• 從優化角度理解機器學習
• 優化技術的重要性
• 常見的凸優化問題
• 線性規劃以及Simplex Method
• Two-Stage LP
• 案例：運輸問題講解

第二周：凸函數講解

• 凸集的判斷
• First-Order Convexity
• Second-order Convexity
• Operations Preserve Convexity
• 二次規劃問題（QP)
• 案例：最小二乘問題
• 項目作業：股票投資組合優化

第三周：凸優化問題

• 常見的凸優化問題類別
• 半定規劃問題
• 幾何規劃問題
• 非凸函數的優化
• 松弛化（Relaxation）
• 整數規劃（Integer Programming)
• 案例：打車中的匹配問題

第四周：對偶（Duality）

• 拉格朗日對偶函數
• 對偶的幾何意義
• Weak and Strong Duality
• KKT條件
• LP, QP, SDP的對偶問題
• 案例：經典模型的對偶推導及實現
• 對偶的其他應用

第五周：優化技術

• 一階與二階優化技術
• Gradient Descent
• Subgradient Method
• Proximal Gradient Descent
• Projected Gradient Descent
• SGD與收斂
• Newton’s Method
• Quasi-Newton’s Method

第二部分 圖神經網絡

第六周：數學基礎

• 向量空間和圖論基礎
• Inner Product, Hilbert Space
• Eigenfunctions, Eigenvalue
• 傅里葉變化
• 卷積操作
• Time Domain, Spectral Domain
• Laplacian, Graph Laplacian

第七周：譜域的圖神經網絡

• 卷積神經網絡回歸
• 卷積操作的數學意義
• Graph Convolution
• Graph Filter
• ChebNet
• CayleyNet
• GCN
• Graph Pooling
• 案例：基于GCN的推薦

第八周：空間域的圖神經網絡

• Spatial Convolution
• Mixture Model Network (MoNet)
• 注意力機制
• Graph Attention Network(GAT)
• Edge Convolution
• 空間域與譜域的比較
• 項目作業：基于圖神經網絡的鏈路預測

第九周：圖神經網絡改進與應用

• 拓展1: Relative Position與圖神經網絡
• 拓展2：融入Edge特征：Edge GCN
• 拓展3：圖神經網絡與知識圖譜: Knowledge GCN
• 拓展4：姿勢識別：ST-GCN
• 案例：基于圖的文本分類
• 案例：基于圖的閱讀理解

第三部分 強化學習

第十周：強化學習基礎

• Markov Decision Process
• Bellman Equation
• 三種方法：Value，Policy，Model-Based
• Value-Based Approach: Q-learning
• Policy-Based Approach: SARSA

第十一周：Multi-Armed Bandits

• Multi-Armed bandits
• Epsilon-Greedy
• Upper Confidence Bound (UCB)
• Contextual UCB
• LinUCB & Kernel UCB
• 案例：Bandits在推薦系統的應用案例

第十二周：路徑規劃

• Monte-Carlo Tree Search
• N-step learning
• Approximation
• Reward Shaping
• 結合深度學習：Deep RL
• 項目作業：強化學習在游戲中的應用案例

第十三周: 自然語言處理中的RL

• Seq2seq模型的問題
• 結合Evaluation Metric的自定義loss
• 結合aspect的自定義loss
• 不同RL模型與seq2seq模型的結合
• 案例：基于RL的文本生成

第四部分 貝葉斯方法

第十四周：貝葉斯方法論簡介

• 貝葉斯定理
• 從MLE, MAP到貝葉斯估計
• 集成模型與貝葉斯方法比較
• 計算上的Intractiblity
• MCMC與變分法簡介
• 貝葉斯線性回歸
• 貝葉斯神經網絡
• 案例：基于Bayesian-LSTM的命名實體識別

第十五周：主題模型

• 生成模型與判別模型
• 隱變量模型
• 貝葉斯中Prior的重要性
• 狄利克雷分布、多項式分布
• LDA的生成過程
• LDA中的參數與隱變量
• Supervised LDA
• Dynamic LDA
• LDA的其他變種
• 項目作業：LDA的基礎上修改并搭建無監督情感分析模型

第十六周：MCMC方法

• Detailed Balance
• 對于LDA的吉布斯采樣
• 對于LDA的Collapsed吉布斯采樣
• Metropolis Hasting
• Importance Sampling
• Rejection Sampling
• 大規模分布式MCMC
• 大數據與SGLD
• 案例：基于分布式的LDA訓練

第十七周：變分法（Variational Method)

• 變分法核心思想
• KL散度與ELBo的推導
• Mean-Field變分法
• EM算法
• LDA的變分法推導
• 大數據與SVI
• 變分法與MCMC的比較
• Variational Autoencoder
• Probabilistic Programming
• 案例：使用概率編程工具來訓練貝葉斯模型

第十八周：其他前沿主題

• 模型的可解釋性
• 解釋CNN模型
• 解釋序列模型
• Meta Learing
• Fair Learning
• 技術前瞻

課程其他的細節可以聯系課程顧問來獲取
添加課程顧問小姐姐微信
報名、課程咨詢

02 部分案例和項目

運輸優化問題：在運籌學以及優化領域最為經典的問題之一，類似的思想廣泛應用在倉庫優化，匹配等問題上。

涉及到的知識點：

• 線性回歸以及優化實現
• Two-Stage隨機線性規劃一下優化實現

打車中的路徑規劃問題：我們幾乎每天都在使用打車軟件或者外賣軟件。對于這些應用來講，核心算法應用就是乘客和車輛的匹配。

涉及到的知識點：

• Mixed Integer Linear Programming
• 提供approximation bounds

經典機器學習模型的對偶推導及實現：通過此練習，更深入理解機器學習模型以及對偶的作用。

涉及到的知識點：

• SVM，LP等模型
• 對偶技術
• KKT條件

基于圖神經網絡的文本分類：當使用語法分析工具處理文本之后，一段文本便可以成為一個圖，接下來就可以使用圖卷積神經網絡來做后續的分類工作

涉及到的知識點：

• 語法分析
• 圖神經網絡

基于圖神經網絡的閱讀理解：一般的閱讀需要讓機器閱讀多個文章并對提出的問題給出答案。在閱讀理解中抽取關鍵的實體和關系變得很重要，這些實體和關系可以用來構造一個圖。

涉及到的知識點：

• 命名識別，關系抽取
• 圖神經網絡
• Heterogeneous Graph

Bandits在推薦系統的應用案例：Bandits應用在順序決策問題的應用中有易于實現、計算效率高、解決冷啟動問題、數據標注相對要求不高（一般只需部分標注作為reward，如用戶點擊）等優點。本案例講解bandits如何應用在新聞推薦的系統中做基于內容的推薦。

涉及到的知識點：

• Exploration & Exploitation
• Epsilon Greedy
• Upper Confidential Bounder
• LineUCB

使用概率編程工具來訓練貝葉斯模型：類似于Pytorch，Tensorflow，概率編程工具提供了對貝葉斯模型的自動學習，我們以LDA等模型為例來說明這些工具的使用。

涉及到的知識點：

• 概率編程
• 主題模型
• MCMC和變分法

股票投資組合優化：在投資組合優化中，我們需要根據用戶的風險承受能力來設計并組合資產。在本項目中，我們試著在二次規劃的框架下做一些必要的修改如加入必要的限制條件、必要的正則來控制組合的稀疏性、加入投資中的先驗等信息，最后根據預先定義好的評估標準來引導模型的學習

涉及到的知識點：

• 二次規劃
• 不同的正則使用
• 基于限制條件的優化
• 先驗的引入

課程其他的細節可以聯系課程顧問來獲取
添加課程顧問小姐姐微信
報名、課程咨詢

03 授課導師

李文哲：貪心科技創始人兼CEO，人工智能和知識圖譜領域專家，曾任金融科技獨角獸公司的首席科學家、美國亞馬遜的高級工程師，先后負責過聊天機器人、量化交易、自適應教育、金融知識圖譜等項目，并在AAAI、KDD、AISTATS等頂會上發表過15篇以上論文，并榮獲IAAI，IPDPS的最佳論文獎，多次出席行業峰會發表演講。分別在USC, TAMU，南開攻讀博士、碩士和本科。

楊棟：香港城市大學博士, UC Merced博士后，主要從事于機器學習，圖卷積，圖嵌入的研究。先后在ECCV, Trans on Cybernetics, Trans on NSE, INDIN等國際頂會及期刊上發表過數篇論文。

04 直播授課，現場推導演示

區別于劣質的PPT講解，導師全程現場推導，讓你在學習中有清晰的思路，深刻的理解算法模型背后推導的每個細節。更重要的是可以清晰地看到各種模型之間的關系！幫助你打通六脈！

▲源自：LDA模型講解

▲源自：Convex Optimization 講解

▲源自：Convergence Analysis 講解

05 課程安排（以前兩周為例）

06 前兩期學員背景

07 入學標準

1、理工科專業相關本科生、碩士生、博士生。
2、目前從事AI工作。
3、具備良好的Python編程能力。
4、具備一定機器學習基礎，零基礎學員不太適合。

08 報名須知

1、本課程為收費教學。
2、本期僅招收剩余名額有限。
3、品質保障！正式開課后7天內，無條件全額退款。
4、學習本課程需要具備一定的機器學習基礎。

—?完?—