蘇州大學(xué)首篇數(shù)學(xué)四大刊！解決了40年未決的丟番圖逼近問題

聞樂 2025-12-15 12:16:09 來源：量子位

聞樂 發(fā)自 凹非寺

量子位 | 公眾號(hào) QbitAI

中國(guó)學(xué)者又一篇數(shù)學(xué)四大刊成果出爐，還是蘇州大學(xué)的首篇四大刊成果。

論文《Khintchine dichotomy for self-similar measures》已被Journal of the American Mathematical Society（《美國(guó)數(shù)學(xué)雜志》）錄用。

該項(xiàng)成果的作者是蘇州大學(xué)副教授張涵，合作者有Timothée Bénard?（法國(guó)國(guó)家科學(xué)研究中心 (CNRS)，巴黎北索邦大學(xué) (LAGA) 的研究員）和何偉鯤?（中國(guó)科學(xué)院數(shù)學(xué)與系統(tǒng)科學(xué)研究院副研究員）。

《數(shù)學(xué)年刊》《數(shù)學(xué)學(xué)報(bào)》《數(shù)學(xué)新進(jìn)展》和《美國(guó)數(shù)學(xué)雜志》并稱為數(shù)學(xué)四大刊，是國(guó)際數(shù)學(xué)界公認(rèn)的數(shù)學(xué)頂級(jí)期刊，每年中國(guó)研究機(jī)構(gòu)中選論文經(jīng)常不超過10篇。

這次的突破是把描述有理數(shù)如何近似表達(dá)實(shí)數(shù)的辛欽定理推廣到了所有自相似測(cè)度上。

接下來咱就看看是怎么個(gè)拓展法。

從勒貝格測(cè)度到所有自相似測(cè)度

要理解這項(xiàng)研究的價(jià)值，首先得先說說兩個(gè)關(guān)鍵概念——辛欽定理和自相似測(cè)度。

辛欽定理是概率論中大數(shù)定律的一個(gè)核心結(jié)論，從理論上揭示了獨(dú)立同分布隨機(jī)變量序列的算術(shù)平均值，會(huì)依概率收斂到其共同的數(shù)學(xué)期望。

也就是解釋了我們?nèi)粘Ｉ钪幸粋€(gè)默認(rèn)的現(xiàn)象：當(dāng)樣本足夠多時(shí)，樣本的平均值會(huì)靠近總體的真實(shí)平均值。

在數(shù)論分支上，它還有一個(gè)重要的應(yīng)用，就是用來描述有理數(shù)逼近實(shí)數(shù)的規(guī)律。

像π這樣的實(shí)數(shù)，沒辦法用一個(gè)有理數(shù)精確表示，但總能找到一個(gè)分?jǐn)?shù)，讓它和這個(gè)實(shí)數(shù)的差距縮小到我們想要的任意精度。

比如用22/7逼近π，誤差不到0.0015；用355/113逼近π，誤差更是能縮小到千萬分之三。

而數(shù)論領(lǐng)域的辛欽定理，就從數(shù)學(xué)層面量化了這種逼近的可能性和效率。它給出了一個(gè)明確的判定規(guī)則，告訴我們什么樣的實(shí)數(shù)，能被有理數(shù)以多快的速度逼近，以及這種高效逼近的有理數(shù)，到底是稀有還是常見。

而這個(gè)判定規(guī)則，關(guān)鍵看一個(gè)特定的逼近函數(shù)ψ的求和是否發(fā)散——發(fā)散則好逼近的點(diǎn)多，收斂則好逼近的點(diǎn)少。

不過，之前辛欽定理多適用于勒貝格測(cè)度，也就是長(zhǎng)度、面積、體積等常規(guī)度量。

而這次論文將其推廣到自相似測(cè)度，關(guān)鍵性質(zhì)是局部與整體的分布規(guī)律相似。

與均勻的勒貝格測(cè)度不同，它會(huì)根據(jù)自相似集合的結(jié)構(gòu)，把測(cè)度質(zhì)量集中在集合的關(guān)鍵部分。

如果把一個(gè)帶有自相似測(cè)度的集合放大或縮小一定比例，得到的局部集合的測(cè)度分布，和原來的整體集合的測(cè)度分布是成比例復(fù)刻的。

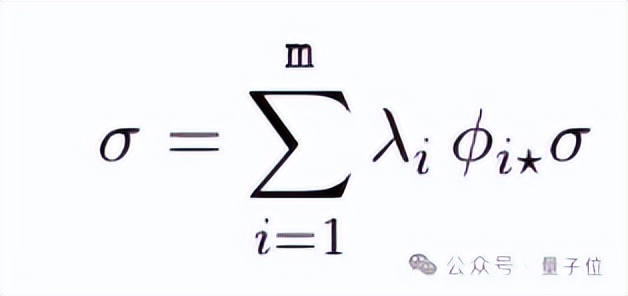
這類測(cè)度廣泛存在于分形幾何、動(dòng)力系統(tǒng)等領(lǐng)域。最典型的例子就是中間三分之一康托爾集（通過無限次三等分線段、去掉中間一段形成的分形）上的測(cè)度。

此次研究通過三個(gè)關(guān)鍵理論支撐實(shí)現(xiàn)了突破。

一是定理A直接確立了自相似測(cè)度下的辛欽二分法，與經(jīng)典定理形式保持一致；

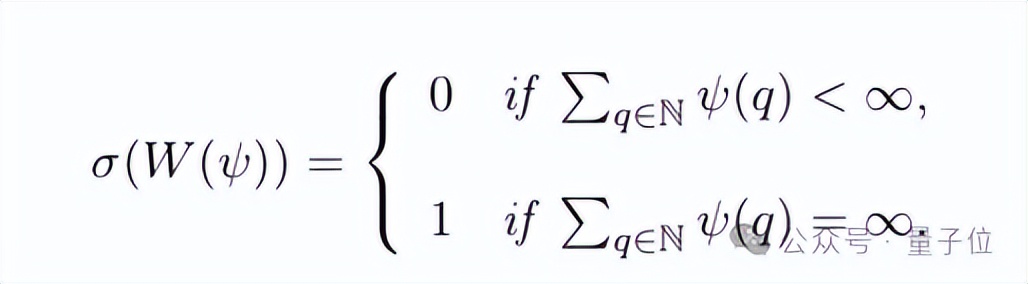
二是定理B證明了自相似測(cè)度在擴(kuò)展變換下的有效等分布，并給出了誤差估計(jì)。

聽著玄，其實(shí)就是隨著變換推進(jìn)，測(cè)度會(huì)越來越均勻地鋪在空間里，而且能算出不均勻的程度有多小，也就是能精準(zhǔn)知道什么時(shí)候能近似均勻分布。

三是定理C通過研究特定隨機(jī)游走的等分布特性，為前兩項(xiàng)定理提供了堅(jiān)實(shí)基礎(chǔ)。

隨機(jī)游走可以理解成：每次按概率選一個(gè)方向走一步，多次后形成的軌跡分布。

定理C證明這種隨機(jī)游走的軌跡分布，也能實(shí)現(xiàn)有效等分布。

而定理A要的“自相似測(cè)度規(guī)律”、定理B要的“擴(kuò)展變換下的均勻分布”，本質(zhì)上都和“測(cè)度如何隨變換/步數(shù)均勻化”有關(guān)。

定理C先把“隨機(jī)游走的均勻化規(guī)律”搞清楚了，后面定理A和B只需要把自相似測(cè)度放進(jìn)這個(gè)框架里，就能順理成章地推出結(jié)論。

這一系列證明也徹底解決了1984年數(shù)學(xué)家Mahler提出的康托爾三分集上的丟番圖逼近問題。

這個(gè)問題的核心就是想知道分形上的無理數(shù)能否被有理數(shù)有效逼近，以及逼近規(guī)律是否與普通線段一致。

如今，論文給出了明確答案：分形與普通線段的逼近規(guī)律完全相同，依然由ψ函數(shù)的求和斂散性決定。

這項(xiàng)成果打通了齊次動(dòng)力系統(tǒng)、分形幾何、數(shù)論三大領(lǐng)域的研究路徑，為后續(xù)交叉學(xué)科研究提供了重要借鑒。

作者介紹

Timothée Bénard， 是法國(guó)國(guó)家科學(xué)研究中心（CNRS），巴黎北索邦大學(xué)?（LAGA）?的研究員。

研究興趣在于李群及其離散子群商群上的隨機(jī)游走，研究領(lǐng)域主要是概率論、動(dòng)力系統(tǒng)、調(diào)和分析和李群理論。

何偉鯤，2017年博士畢業(yè)于巴黎第十一大學(xué)。

隨后分別在耶路撒冷希伯來大學(xué)與韓國(guó)高等研究院任博士后。

2022年初入職中國(guó)科學(xué)院數(shù)學(xué)與系統(tǒng)科學(xué)研究院，任副研究員。研究興趣包含齊次動(dòng)力系統(tǒng)、分形幾何、幾何。

張涵，博士畢業(yè)于俄亥俄州立大學(xué)，后進(jìn)入清華大學(xué)進(jìn)行博士后研究。

2023年10月入職蘇州大學(xué)，被聘為校優(yōu)秀青年學(xué)者、特聘副教授，研究方向?yàn)辇R性動(dòng)力系統(tǒng)及其在數(shù)論中的應(yīng)用。

論文地址：https://arxiv.org/abs/2409.08061
參考鏈接：https://math.suda.edu.cn/74/62/c10866a685154/page.htm

— 完 —