半世紀難題48小時破解！陶哲軒組隊把AI數學玩成打怪游戲了

鷺羽 2025-12-13 22:43:25 來源：量子位

西風 鷺羽 發自 凹非寺

量子位 | 公眾號 QbitAI

剛剛，陶哲軒與多名數學家通力合作，為Erd?s#1026正式畫上了句號。

至此，這個塵封50年的難題終于得到完全解決。

關鍵是，AI又立大功了。在多種AI工具的輔助下，整個解題流程僅用48小時便完成。

博采眾家&AI之長，正在成為解決問題的關鍵。

正如陶哲軒本人所說：

用傳統方法，一兩位數學家用簡單的編程和文獻檢索工具，最終也能完成，但可能需要數周或者數月才能解決。

陶哲軒隨后親自梳理并公開了此次問題被解決的完整過程。

消息傳出后，網友紛紛感嘆“太酷了”：

一起來看看他們究竟是如何解決的？

48小時解決Erd?s#1026

Erd?s#1026問題最早在1975年被提出，初始問題為：

但該問題表述相當模糊，于是數學家Desmond Weisenberg提議對這個函數的最小可能值進行研究，引入一個最大常數的量c(n)，使得：

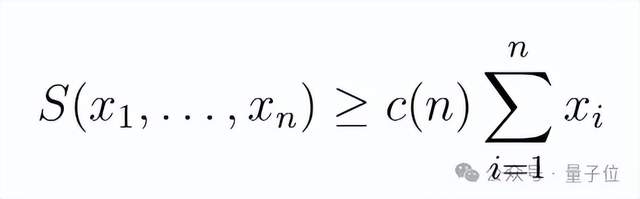
其中c(n)是所有長度為n的不同實數序列。

如果用博弈論來解釋該問題，那么就是：

問Bob無論Alice如何分配硬幣，至少能保證拿走全部硬幣的多少比例？其中c(n)是Bob拿走的最小比例。

這里陶哲軒還用AI畫了一張簡單的說明圖：

陶哲軒隨即給出了他的初步答案，顯然c(1)=1時，Alice只有一堆，Bob可以拿走全部；c(2)=1時，兩堆一定處于單調，Bob可以拿兩堆；c(3)=2/3時，Bob至少可以取兩堆，但無法保證全部三堆。

數學家Stijn Cambie提出了更進一步的猜想。

通過計算c(n)的前幾個值可以得到，存在以下近值：1，1，2/3，1/2，1/2，3/7，2/5，3/8，1/3。

該證明成功將原問題轉化為一個計算幾何領域的矩形填充問題。

一個小時不到，另一位數學家Koishi Chan加入其中，給出了一個基于原始Erd?s–Szekeres定理的替代證明，印證了前面AI的發現。

第二天，陶哲軒注意到了這個問題，他將該問題放入AlphaEvolve，要求它通過生成總和為固定值（這里選擇的是10的6次方）的實數（或整數）序列，來獲取c(n)的上界，并盡可能確保S的值夠小。

在運行一小時后，AlphaEvolve生成了以下c(n)的上界，其中包含了一些結構清晰的潛在極值解：

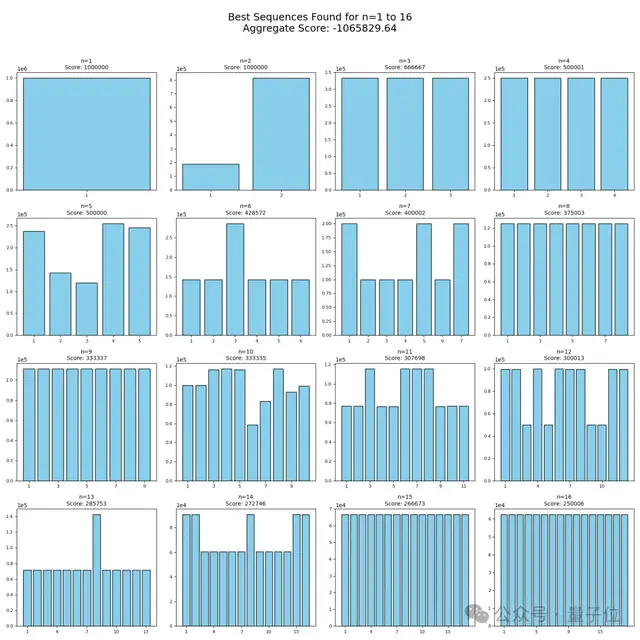
顯然數值分數（除以10的6次方）正在試圖逼近簡單有理數，于是陶哲軒又利用John Cook的公開專用工具，將序列整理成：

這為序列c(n)的值提供了一種猜想，之后Boris Alexeev繼續找到了該猜想的簡潔表述，即：

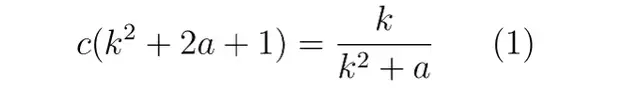
另外，他還提供了一個明確的上界構造：

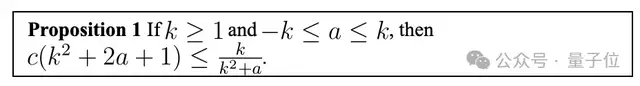
該上界通過構造不利配置的序列實現，基本思想仍然來自Erd?s–Szekeres定理，即復雜設計數字排列順序，會使得長單調序列無法同時擁有很好的權重。

這種構造是組合性的，需要精心設計序列結構與分塊策略，才能使最長序列單調和受限。

用ChatGPT Pro生成1/c(n)的圖像，能夠直觀看出，它基本上是對平方根函數的分段線性逼近。

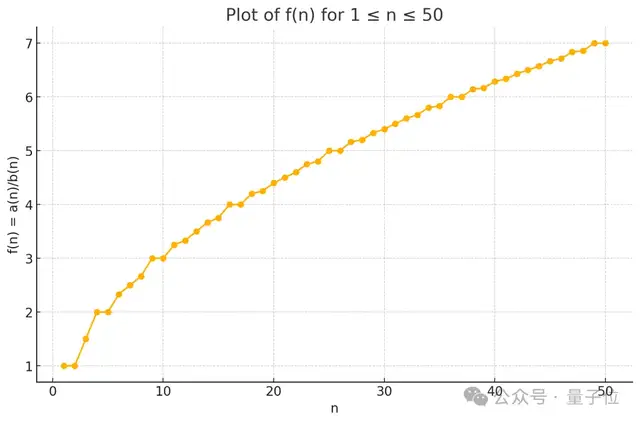
不久之后，數學家Lawrence Wu就該問題，結合正方形填充（Erd?s#106）進行了闡述。

根據Erd?s#106，他將f(n)引入該問題，設定其為最小數，使得把n個正方形按平行坐標軸打包進一個大正方形時，滿足：

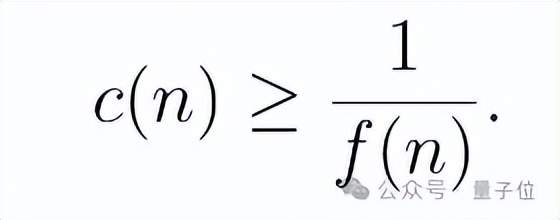
其中對于n=10時，用ChatGPT Pro生成轉換成方形打包的圖像，如圖所示：

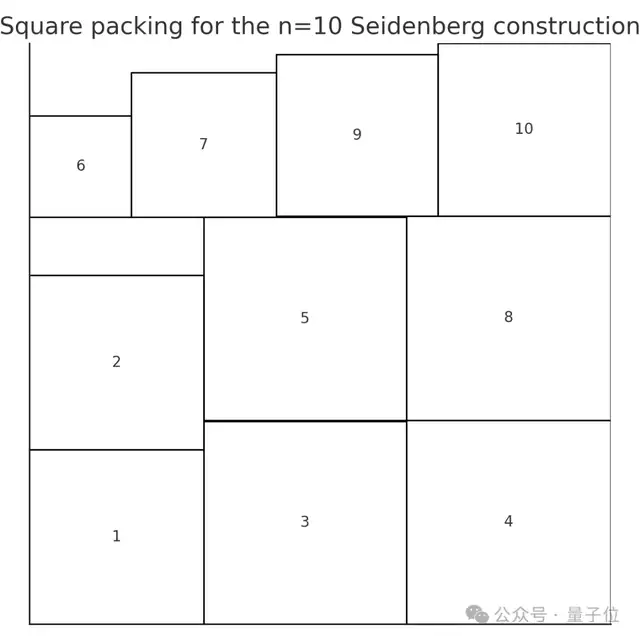
在此基礎上，Lawrence Wu通過AI論文檢索，找到了一篇去年由Baek、Koizumi和Ueoro聯合發表的論文，最終證明了猜想中的公式，從而完成了整體證明。

接下來陶哲軒將上述所有信息全部輸入了ChatGPT，生成了連貫證明。

人+人+AI=數學破壁機

當然，這已經不是陶哲軒第一次用AI解題了。

最近，他還借助Gemini 2.5 Deep Think破解了Erd?s問題#367。

這是他本人很擅長的連續整數結構的乘法數論問題，該問題建立在前人并不完整的反證基礎上，陶哲軒借助Gemini Deep Think進行證明補全。

全程只用了十分鐘，Gemini就從論證分析打通了結論確認。

另外，陶哲軒前段時間還利用GPT-5進行半自動化文獻檢索。

他借助GPT-5對相關數列進行高精度計算，隨后將得到的結果輸入OEIS（一個收錄全球數列的數據庫）進行檢索對照，進而發現部分Erd?s問題其實早已在既有研究中被解決——只是長期沒人注意到，未把結果與問題庫對應起來。

至于什么是Erd?s問題？

它出自20世紀著名匈牙利數學家Paul Erd?s。此人一輩子合作了超500位數學家，畢生發表了約1525篇數學論文，數量之多，至今無人能及。相應地，他也提出或轉述了千道問題，給后人留下了“Erd?s問題”。

其中大量題目被收錄于erdosproblems.com網站。該網站由數學家Thomas Bloom制作，記錄了每道題目的當前狀態。目前，絕大多數難題依然懸而未解。

隨著AI技術的不斷進步，接連有人利用AI成功解答了這些幾十年來未曾解決的難題。

陶哲軒本人就表示，“在Erd?s問題網站上，AI輔助已經變得很常見”。

就在前幾天，來自Harmonic的數學AI模型還被曝獨立證明了Erd?s問題#124。

微軟前AI副總裁、目前在OpenAI研究AGI的Sebastien Bubeck表示“該解決方案100%由AI生成，總計耗時6小時”。

目前，Erd?s網站也公開鼓勵大家借助AI等工具輔助解題：

允許使用AI輔助撰寫評論，但需滿足：(a)公開說明使用了AI；(b) 內容（包括數學內容、代碼、數值數據及相關來源）已由用戶本人獨立（不借助AI）仔細檢查和驗證；(c)評論長度合理。

而這次Erd?s#1026的快速解決，離不開“人與人的協作”+“人與AI的協作”。

這種協作方式，也正在成為一種新趨勢。

參考鏈接：
[1]https://www.erdosproblems.com/forum/thread/1026
[2]https://terrytao.wordpress.com/2025/12/08/the-story-of-erdos-problem-126/