沉浸式線性代數(shù)教材,不懂哪里點哪里,網(wǎng)友:天花板級別
對初學(xué)者也十分友好
克雷西 發(fā)自 凹非寺
量子位 | 公眾號 QbitAI
線性代數(shù)太抽象學(xué)不懂?沒關(guān)系,三名來自瑞典的學(xué)者,為我們帶來了沉浸式的教程。
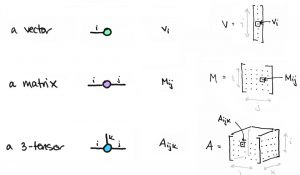
從向量到矩陣、從概念到運算,幾乎每個知識點都配有可以交互的圖片,哪里不會點哪里。

而且部分配套案例還充分結(jié)合實際,用生活場景把專業(yè)概念解釋得明明白白。

對于采用這種形式的原因,作者在序言中表示,他們始終堅信圖片能比文字更加簡潔有效地傳遞信息:
A picture says more than a thousand words.(一圖勝千言。)
這份教程則是在此基礎(chǔ)之上更進一步,交互式的學(xué)習(xí)過程相比于靜態(tài)配圖,進一步提升了學(xué)習(xí)體驗。
這也讓它被網(wǎng)友稱為“線性代數(shù)教材的天花板”,游戲公司Odd Tales的創(chuàng)始人也評價說它是“Pure gold”。
當然只有形式新穎是不夠的,這份教程在內(nèi)容上也是相當翔實,下面就一起了解下吧!
交互式學(xué)習(xí),還有實用案例
首先,這份教材可以說對初學(xué)者十分友好,在開篇專門用了一個章節(jié)快速回顧了三角函數(shù)等知識點。
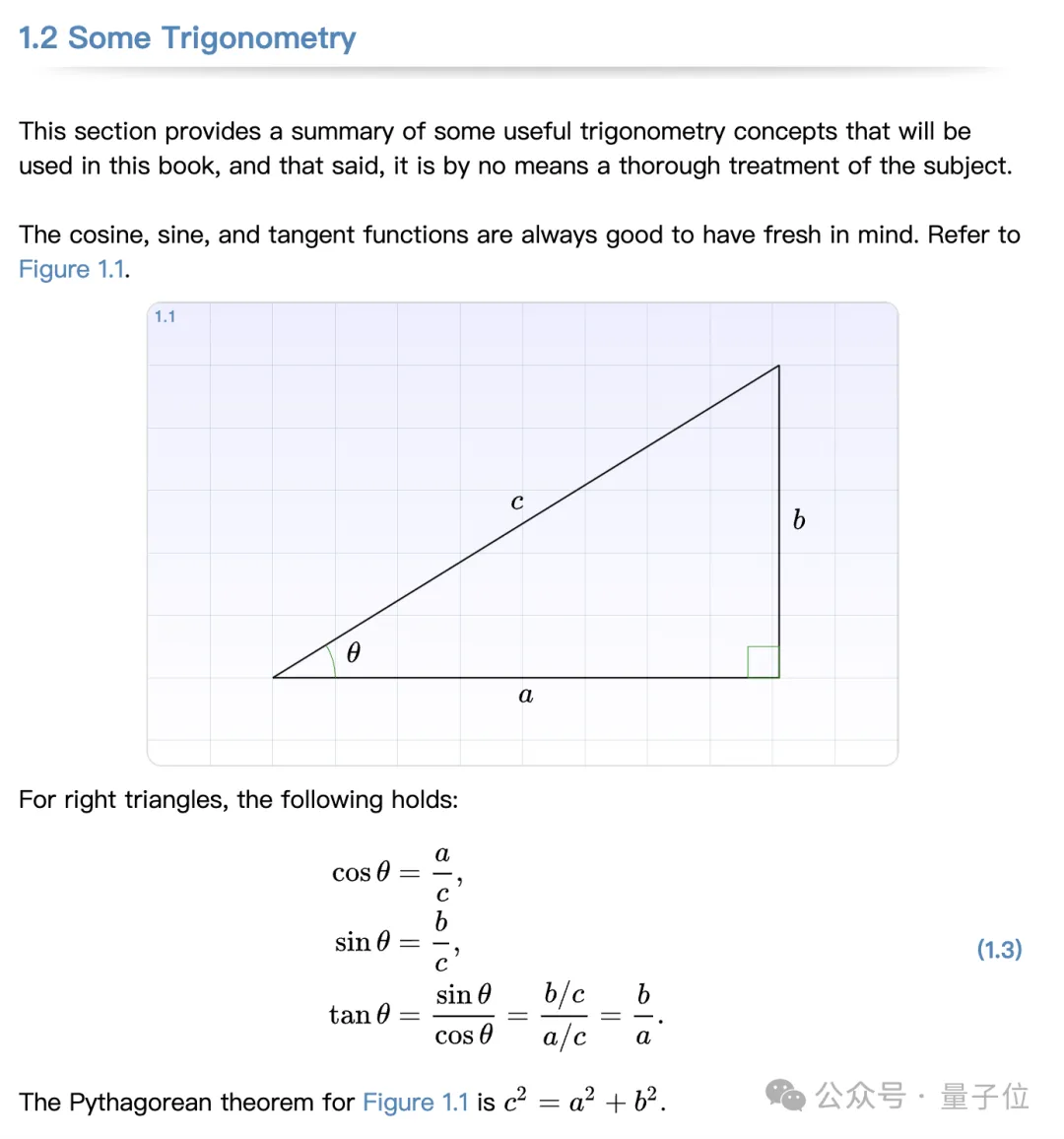
快速喚起這些知識儲備之后,就進入正式學(xué)習(xí)了。
這份教程以向量為出發(fā)點,用了一個打磚塊的小游戲解釋了向量的概念。
在其他章節(jié)的開頭同樣配有這種簡單的例子,作者介紹,只要記住這些例子,就能很輕松地理解主題。

概念明晰之后,就是加、減、數(shù)乘等基本運算,同時還介紹了基向量、高維向量空間等概念。
接下來的兩個章節(jié)也都和向量運算有關(guān),分別介紹了數(shù)量積(內(nèi)積/點乘)和向量積(外積/叉乘)。

值得一提的是,在教程中還配備了實際案例,比如在點乘這部分就講述了如何用向量來探究物理學(xué)中光的反射定律。
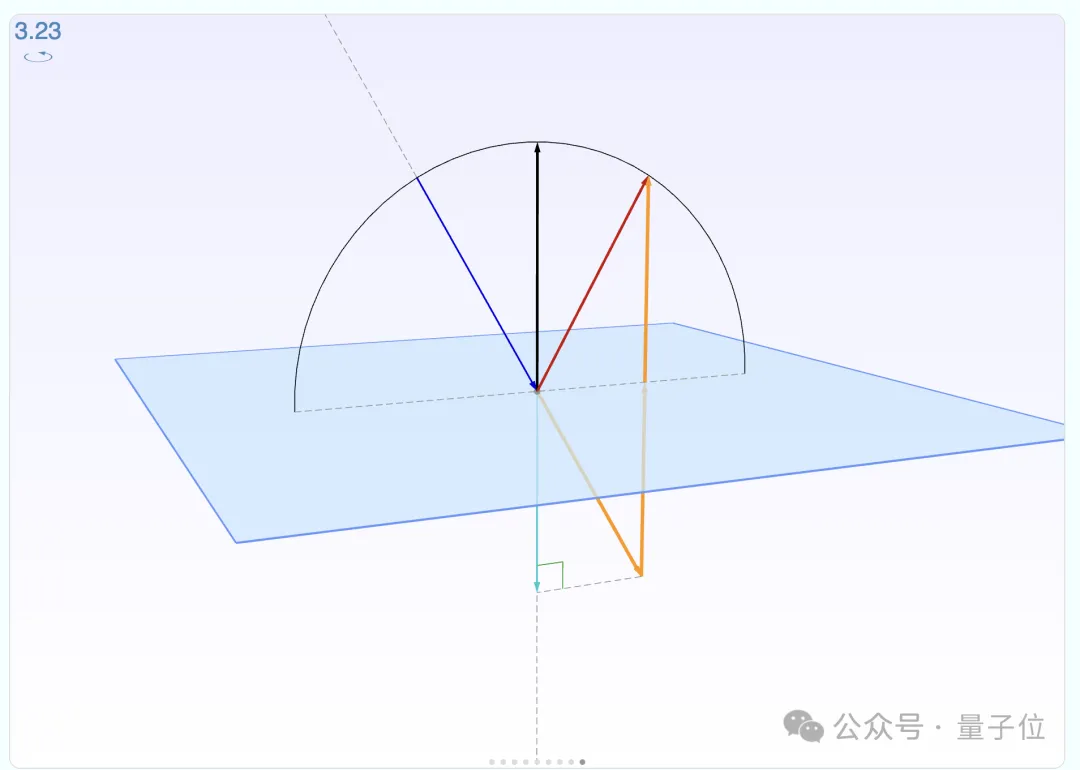
學(xué)(復(fù))習(xí)完這些向量知識之后,就要向著更加復(fù)雜的矩陣邁進了。
不過在此之前還需要再了解一個重要工具——高斯消元,它被用于求解線性方程組,而線性方程組的解析又是理解和使用矩陣的基礎(chǔ)。
在介紹高斯消元時,作者一共用了將近9000個單詞,還舉了非常前沿的例子——計算機視覺——在該領(lǐng)域中,3D模型的建立就與線性方程組求解有關(guān)。

后面的五章內(nèi)容就全都和矩陣相關(guān)了,包括基本概念、行列式、秩、線性規(guī)劃、特征值與特征向量等內(nèi)容。

作者簡介
這套教材的三名作者全都來自瑞典。

其中Tomas Akenine-M?ller和Kalle ?str?m都是隆德大學(xué)教授,分別任教于計算機系和數(shù)學(xué)系。
Tomas于2004年被隆德大學(xué)聘用為助理教授,2007年晉升為教授,從2008年起先后在英特爾和英偉達兼任圖形學(xué)研究者。
另一名作者Jacob Str?m,現(xiàn)在在瑞典通信設(shè)備廠商愛立信擔任首席研究員,他過去的經(jīng)歷也與隆德大學(xué)有關(guān)。
而關(guān)于創(chuàng)作這套教程的目的,作者們這樣說:
我們?nèi)齻€用了20年的線性代數(shù)之后,萌生了寫一本教材的想法,想要讓學(xué)習(xí)和教授線性代數(shù)變得更加容易。
同時,互聯(lián)網(wǎng)技術(shù)也達到了一定的門檻,讓這本書可以以一種非常新穎和創(chuàng)新的方式呈現(xiàn)。
如果你認可這套體系和學(xué)習(xí)方式,不妨給自己安排安排,傳送門就在下邊了。
傳送門:
https://immersivemath.com/ila/
- 論文自動變漫畫PPT!Nano Banana同款用秘塔免費生成,還有一對一語音講解2025-12-09
- 高通萬衛(wèi)星:混合AI與分布式協(xié)同是未來 | MEET20262025-12-11
- 智能體A2A落地華為新旗艦,鴻蒙開發(fā)者新機遇來了2025-12-06
- 14歲華人小孩,折個紙成美國天才少年2025-12-06