陶哲軒用GPT5-Pro跨界挑戰！3年無解的難題，11分鐘出完整證明

鷺羽 2025-10-11 12:18:50 來源：量子位

夢晨 鷺羽 發自 凹非寺
量子位 | 公眾號 QbitAI

陶哲軒與GPT-5 Pro這對搭檔再大發神威，解決了一個3年無人解決的難題。

而且是“不太在自己專業范圍內”的問題：微分幾何領域的開放問題。

要知道，陶哲軒擅長的分析、數論、組合學等研究的往往是整數、函數、算子的性質。而微分幾何更側重于流形的性質，常用的工具也很不一樣。

陶哲軒只是按自己直覺給了一個大致方向，GPT-5 Pro就從復雜計算到嚴謹證明一氣呵成，幫助陶哲軒捕捉關鍵邏輯，突破傳統思維局限。

甚至在AI幫助下最終發現自己的直覺有誤，但通過這個過程更好理解了問題。

有了這次跨界解題的經驗，陶哲軒對AI在學術研究上的作用也有了新的思考，他總結到：

AI在小尺度上很有用，中尺度上有些無益，大尺度上又有幫助。

AI從計算到證明一氣呵成

先來看看原始問題，是3年前就在mathoverflow上提出的：

設一個三維空間中的光滑拓撲球面圍成的區域，且曲面的主曲率絕對值不超過1，那么它包圍的體積是否至少等于單位球的體積？

陶哲軒最初的思路是將問題限制在星形區域上，借助積分不等式推進。但他的微分幾何有些生疏，所以請AI幫他進行這些計算。

結果GPT-5 Pro思考了11分18秒，不僅完成了所有計算，還直接給出了星形情況下問題的完整證明。

證明過程運用了各種不等式和恒等式，其中有些陶哲軒熟悉（比如Stokes定理和Willmore不等式），也有一個他也第一次接觸的Minkowski第一積分公式。

有了這些不等式，加上算術-幾何平均不等式，星形情況的證明實際上就是一行論證。

到目前為止，一切順利。

接下來他需要驗證證明的各個步驟，但網絡上沒有找到有用的資源。

再次詢問AI后，直接得到兩個令他滿意的證明：一個是按照他建議使用散度定理的路線，另一個是基于他沒想到的流方法。

通過AI的計算和證明，陶哲軒打算將其視為一個擾動橢圓偏微分方程問題，AI在這個思路上表現也良好。

雖然在估計一個擾動非線性項時出現了輕微的錯誤，但并非無法修復。而且AI還主動指出一個特殊情況其實又能回到星形的結果。

成功地用偏微分方程擾動理論的方法，解決了當曲面形狀與單位球面差距不大（Small Data）時的情形。

但真正困難且未解決的，是當曲面形狀與球面差距巨大（Large Data）時的問題。

陶哲軒意識到可以用將問題簡化為一個大型有限計算，但AI用這個方法給出的結果非常混亂且缺乏啟發性，本質上是對所有可能形狀的窮舉。

最終陶哲軒發現他設想的數值方法或許可以在有限的時間內解決所有給定條件的特殊情況，但無法處理一般情況，但AI只是按照提問照做了。

最后總結一下：雖然問題最終還是沒有完全解決，但在AI的幫助下陶哲軒對這個問題的理解深入了很多。

陶哲軒的思考：AI工具的多尺度價值

雖然解題告一段落，但陶哲軒的思考還在繼續。

回顧整個解題過程，AI在“小尺度”問題上表現得很好，只犯了一些小錯誤，并貢獻了一些文獻中已有的，但陶哲軒之前并不知道的有用想法。

但是要想進一步推進這個問題，就需要真正的微分幾何專家的幫助了。

在“中等尺度”的策略上，AI略微顯得無益，它強化了陶哲軒對問題的錯誤直覺，而不是提出質疑。

陶哲軒一開始的直覺是錯的，AI也沒有發現問題，基本上只是附和同意他說的一切。

但是在從獲得對問題理解的“大尺度”指標來看，AI又是有幫助的，盡管主要是間接意義上的：在AI的幫助下能夠更快地研究并最終放棄一種現在認為不適合的方法。

陶哲軒將這次經歷與他之前的實驗進行了對比。

在之前的實驗中，他給AI一個他對結果有很好直覺的任務。這種情況下AI更有創造力，提供了他不知道的信息，但引導AI朝著富有成效的方向前進也明顯更加困難。

他認為，在自己專業領域之外的問題上與AI互動似乎確實有一些價值，但必須謹慎行事并保持對情況的認知。

這次經歷還印證了陶哲軒之前提出的觀點：必須在多個尺度上衡量一個工具的有效性。

此前他提出了四個不同的效率衡量尺度：形式化證明中的任何單行、任何單個引理、任何定理的完整證明，以及整本教科書。

許多當前的自動化工具可以在其中一個尺度上加速形式化，但反直覺的是，過度依賴這樣的工具可能最終會降低在其他尺度上形式化的能力。

他認為最優的自動化水平實際上嚴格介于0%和100%之間。

在每個尺度上都有足夠的自動化來減少繁瑣的重復工作，但在每個尺度上仍然有足夠的”人在回路中“來審查和修復局部問題，以便讓人類保持對所有尺度上任務結構的感知。

如果過度地在單一尺度上對AI進行基準測試，最終可能會對長期目標產生不利影響。

陶哲軒與ChatGPT合作史

而陶哲軒對AI輔助數學工作的可能性探索還要追溯到三年前——ChatGPT剛剛發布的時候。

陶哲軒在其誕生伊始就敏銳地察覺到它的作用，并就黎曼假設進行試探性詢問，但得出的結果卻讓他大失所望：

ChatGPT給出了看似合理且相關的回答，但仔細檢查后卻沒有任何實際的深度內容。

此時的ChatGPT還不能完全理解數學問題的本質，只是在將一些低質量內容進行包裝掩蓋，這意味著常規的表面檢測方法不再準確，需要對核心內容進行人工篩查，例如逐行地閱讀文本。

所以早期的陶哲軒對AI工具抱有懷疑審視的態度，認為AI在數學中的作用，是為答案提供近似值，然后人類數學家再通過傳統方法進行逐步細化。

轉機出現在GPT-4，陶哲軒嘗試使用GPT-4協助處理統計數據，即把原始數據輸入電子表格，并查找對應函數、計算所需內容。

短短幾分鐘，GPT-4就完成了人類一天的工作，期間只有非常少的部分需要校驗，這也讓陶哲軒開始期待將AI集成到軟件工具中，尤其是處理90%以上的LaTeX編譯問題。

我可以明確地說，今天是GPT4為我節省了大量繁瑣工作的第一天。

隨后，他開始使用GPT-4處理一些自己熟悉領域的數學問題，比如下面這個問題：證明遞歸式（定義R）能夠推導出a(n+1)。

GPT4從合作者的角度提出了八種不同方法，其中生成函數法引起了陶哲軒的注意，并隨即沿著該解決路徑，利用人工計算最終解決了這個問題。而最初陶哲軒想使用的是漸近分析方法，但事實證明AI可以更快地協助找到正確方案。

與此同時，他開始讓ChatGPT編寫Python來計算序列長度，雖然與預期的目標序列存在差異，只考慮到了連續整數的子序列而非任意子序列，但已經足夠接近，而且其中在計算totient函數時還使用了非常獨到的方案。

但代碼本身有時也不夠簡潔、效率不高，或者邏輯不夠嚴密，還是需要人工校正與重寫。

他還嘗試使用Copilot書寫數學論文，不過在攥寫證明大綱時，AI陷入了長篇敘述有關隨機分析數論的廢話，只有在編寫非常短或重復的文本上有效。

所以此時的AI在陶哲軒看來，AI寫數學論文仍然是有趣多過于有用。

在GPT-o1發布后，陶哲軒同樣第一時間測試了其數學能力，顯然相比于前代，GPT-o1的幻覺問題得到解決，在形式化任務中也作用顯著，但在復雜分析問題上仍然令人失望，沒有產生關鍵的概念思想。

陶哲軒將這一代模型定義為平庸但并非完全無能的數學“研究生”，而此前的模型則更接近為無能的“研究生”水平，不過他也相信再迭代一兩次，加上與其他工具的集成，AI將在研究級別的任務中大有所為。

而今年七月份，OpenAI斬獲IMO金牌一事讓AI的數學能力再次引起熱議，陶哲軒也對此做出了長文回應，認為缺乏統一的評測標準。

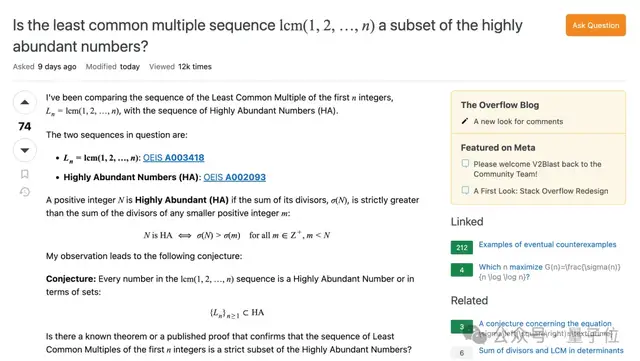
但同時他也開始讓ChatGPT處理一些更為復雜的數學問題，比如在判斷該集合是否是HA的子集時，陶哲軒通過理論分析已經確定該問題的答案是否定的，但仍需要一些數值參數來驗證部分不等式。

起初，直接要求AI提供一個Python代碼的反例，但由于初始參數問題始終失敗，隨后陶哲軒調整策略轉而與AI逐步對話，使其執行啟發式計算并找到可行的參數選擇，通過單獨驗證生成的參數，最終解決了該問題。

陶哲軒總結認為，在數值搜索這類任務上，AI工具顯然可以節省大量時間，如果沒有AI，甚至他可能都不會考慮這種解決方法，而是尋求理論漸進分析。

而對于如何減少AI在數學問題中的幻覺或廢話問題，陶哲軒也顯然有了自己的一套心得，那就是在計算任務的每一步都做到詳細解釋，每一次和AI的對話都先確認再執行下一步，在對話結束后再使用Python進行外部驗證，得到輸出。

正如他一直所說的那樣，AI正在重塑人類科學范式，其最合理的角色是成為數學家的“副駕駛”或助理，而不是取代人類在創造性、直覺性、策略性上的工作。

在AI的協助下，數學將在未來擁有更多的實驗，而不僅僅是理論。

原文地址：https://mathstodon.xyz/@tao/115351400633010670

參考鏈接：
[1]https://chatgpt.com/share/68e85cba-7228-800e-8804-a0f41aa64e14
[2]https://mathoverflow.net/questions/425509/sphere-with-bounded-curvature
[3]https://terrytao.wordpress.com/mastodon-posts/