陶哲軒罕見長長長長長訪談：數(shù)學(xué)、AI和給年輕人的建議

鷺羽 不圓 發(fā)自 凹非寺
量子位 | 公眾號 QbitAI

陶哲軒罕見接受了一次長長長長訪談，把他關(guān)于數(shù)學(xué)、AI、教育和人類智慧的最新認知，都對外分享了。

作為菲爾茲獎得主，陶哲軒一直被認為是當世最偉大的數(shù)學(xué)家之一，而這次在與MIT技術(shù)背景的播客大神Lex Fridman的對話，也是他近年來首次接受超3小時的非學(xué)術(shù)機構(gòu)訪談，內(nèi)容覆蓋數(shù)學(xué)前沿、AI形式化驗證、科研方法論等多個硬核議題。

不僅談?wù)摲窒砹藬?shù)學(xué)和物理相關(guān)的專業(yè)性觀點，還結(jié)合當下AI技術(shù)迅速發(fā)展的背景，作出了很多像基礎(chǔ)教育和AI應(yīng)用的大眾話題思考……

陶哲軒金句頻出，比如：

• AI和菲爾茲獎的距離，只差一個研究生了。
• 復(fù)數(shù)意義上的人類共同體將創(chuàng)造出最頂尖的超級智能體，比單個數(shù)學(xué)家更有可能實現(xiàn)數(shù)學(xué)領(lǐng)域的突破。
• 數(shù)學(xué)的關(guān)鍵在于不僅是找到一個有效的技術(shù)路徑，而是在幾十種可能適用的方法中排除錯誤答案。
• 科學(xué)通常是三者之間的相互作用：現(xiàn)實世界、我們對現(xiàn)實世界的觀察，以及我們認為世界如何運作的模型。
• 在理解和看待世界的方式上，數(shù)學(xué)從公理出發(fā)關(guān)注模型，物理由結(jié)論驅(qū)動注重收集結(jié)果。
• 在AI的協(xié)助下，數(shù)學(xué)在未來將會有更多的實驗，而不僅僅是理論。
• 數(shù)學(xué)之美在于你可以隨心所欲地改變規(guī)則，這是其它任何領(lǐng)域都無法做到的一點。
• 解決困難問題就像香港動作片，逐個擊破，方得大成。

……

陶哲軒認為，AI正在重塑人類科學(xué)范式，數(shù)學(xué)和物理的終極問題上，AI將成為人類探索這些范式的重要伙伴，但無法取代人類的直覺與創(chuàng)造力。

而關(guān)于數(shù)學(xué)，他也深入淺出地談?wù)摿艘韵率澜缂墧?shù)學(xué)難題——

• Kakeya猜想
• 納維-斯托克斯正則性問題
• 塞邁雷迪定理
• 萬物理論
• 廣義相對論
• 龐加萊猜想
• 孿生素數(shù)猜想
• 克拉茲猜想
• 黎曼假設(shè)
• 費馬大定理

嗯，是的，這就是一次高智力、高密度和高強度的三高對話，如果你也做好了“大腦尖叫”的準備，一起來看看我們整理過的訪談全文吧～～

訪談陶哲軒全文

本科教育只需要解決10%的問題

Q：你遇到的第一個真正困難的研究級數(shù)學(xué)問題是什么？

陶哲軒：在本科教育中，你會學(xué)到那些真正困難的、甚至看起來是不可能解決的問題，比如黎曼假設(shè)、孿生素數(shù)猜想。但事實上這并不算什么，真正有趣的是，那些現(xiàn)有技術(shù)能完成大約90%的工作，而你只需要解決剩下10%的問題。

在博士期間，Kakeya問題引起了我的注意，事實上這個問題剛剛得到解決，這也是我在早期研究中投入很多的一個問題。歷史上，它源于日本數(shù)學(xué)家Soji Kakeya在1918年左右提出的一個小謎題。

這個謎題是：假設(shè)你在平面上時有一根針，或者想象成在路上開車時要執(zhí)行一個U型轉(zhuǎn)彎，你想在盡可能小的空間內(nèi)，讓這根針調(diào)轉(zhuǎn)方向。

但這根針的移動是無限的，所以可以把它視作一個圍繞中心旋轉(zhuǎn)的單位指針。這需要一個面積為π/4的圓盤。

或者你可以做一個三點掉頭，實際上只需要π/8的面積。所以，它比旋轉(zhuǎn)更高效。因此，一段時間內(nèi)，人們認為這是調(diào)轉(zhuǎn)指針方向最有效的方法。

但是Besicovitch證明了，事實上可以用任意小的面積來讓這根針掉頭，比如0.001。所以可以有多種花哨的來回掉頭操作，來實現(xiàn)這一點，這樣就能讓針在掉頭過程中穿過每一個中間方向。

這發(fā)生在二維平面上。我們理解二維中的一切，那么接下來的問題是，在三維空間中會發(fā)生什么？

假設(shè)哈勃太空望遠鏡是太空中的一根管子，如果你想觀測宇宙中的每一顆恒星，就需要旋轉(zhuǎn)望遠鏡以指向每一個方向。

做一個不切實際的構(gòu)想：假設(shè)空間非常寶貴，雖然實際并不是如此，你需要占據(jù)盡可能小的體積來旋轉(zhuǎn)你的針，也就是望遠鏡。那么需要多小的體積才能做到這一點？你可以試圖修改基本構(gòu)造，讓望遠鏡厚度為零，這樣就可以使用任意小的體積。

但問題是，如果你的望遠鏡不是零厚度，而是很薄的厚度delta，那么作為delta的函數(shù)，能夠看到所有方向所需的最小體積會是多少？

以及隨著delta變小，針變細，體積也會減小，但下降速度有多快呢？當時的猜想是它下降得非常非常慢，就像呈對數(shù)速度下降，這一點在經(jīng)過大量工作后也得到了證實。

這個問題有趣的點在于，結(jié)果證明它與偏微分方程、數(shù)論、幾何、拓撲學(xué)、組合學(xué)中的許多問題都有著驚人的聯(lián)系。

例如，在波傳播中，當你向周圍潑灑一些水并濺起水波，它們會向周圍各個方向傳播，但波同時表現(xiàn)出粒子和波的行為，得到所謂的“波包”，它在空間中非常局限，并隨著時間向某個方向移動。如果在空間和時間上繪制它，會顯示出一個管狀區(qū)域。

因此可能會出現(xiàn)，一個最初非常分散的波，在稍后的某個時間節(jié)點上，全部聚焦到一點。就像將一顆鵝卵石扔進池塘，漣漪會擴散開。但如果你對該場景進行時間逆轉(zhuǎn)，并且要知道波動方程是時間可逆的，你就可以想象漣漪會匯聚到一個點上，然后發(fā)生巨大的飛濺，甚至可能產(chǎn)生奇點。

從幾何學(xué)上講，光線也是如此。如果這個波代表光，將波看作是光子的疊加，且光子都沿著光線傳播，并且都最終聚焦在一點上。

因此你可以在空間和時間的某個點上，將一個非常分散的波聚焦成一個非常集中的波，但之后它又會再次散開并分離。

但如果該猜想有一個負解，那么這意味著有一種非常高效的方法，可以將指向不同方向的管子打包匯集到一個非常狹窄的小體積區(qū)域。

那么你也將能夠創(chuàng)造出一些波，它們開始時非常分散，但它們最終不僅會集中在一個點上，在時空中也會有大量的集中點，你將創(chuàng)造出所謂的爆炸，波的振幅將變得相當大，以至于它們所依靠的物理定律不再是波動方程，而是更復(fù)雜和非線性的東西。

所以在數(shù)學(xué)和物理中，我們非常關(guān)心某些波動方程是否穩(wěn)定，是否能夠產(chǎn)生奇點。

通過改變物理規(guī)律來制造爆炸

Q：您能否談一下納維-斯托克斯問題？

陶哲軒：有一個著名的未解決問題，叫做納維-斯托克斯正則性問題，即控制水等不可壓縮流體的流動。

問題在于，如果你從一個平滑的水流速度場開始，它是否會集中到如此大的程度，以至于從某一點開始速度變得無窮大，而這一點就是奇點。當然現(xiàn)實生活中我們不會親眼看到。

事實上，近年來人們已經(jīng)達成了共識，對于某些非常特殊的初始構(gòu)型，比如水，可以形成奇點，只是還未能真正證實。

在克萊基金會的七個千禧年問題中，解決其中一個問題就可獲得一百萬美元獎金，而這就是其中之一。當中只有龐加萊猜想已經(jīng)被解決。

所以雖然Kakeya猜想與納維-斯托克斯問題沒有直接聯(lián)系，但理解Kakeya猜想有助于我們理解波集中這樣的問題，這可能會間接幫助我們更好地理解納維-斯托克斯問題。

這就是數(shù)學(xué)家區(qū)別于幾乎所有其他人的地方。如果某件事在99.99%的情況下成立，那么對大多數(shù)事情來說，這就足夠了。但數(shù)學(xué)家會關(guān)心是否100%涵蓋所有情況。大多數(shù)時候，水不會爆炸，但也許能設(shè)計一個非常特殊的初始狀態(tài)讓它爆炸。

克萊獎問題涉及所謂的不可壓縮納維-斯托克斯方程，它控制像水這樣的流體。還有所謂的可壓縮納維-斯托克斯方程，支配像空氣這樣的流體。

在天氣預(yù)報中就有很多流體動力學(xué)計算，需要收集大量數(shù)據(jù)以便能夠初始化納維-斯托克斯方程，甚至盡可能求解它，所以它在實際生活中非常重要。

Q：為什么證明方程的一般性結(jié)論會如此困難？

陶哲軒：舉個例子就是麥克斯韋妖。麥克斯韋妖是熱力學(xué)中的一個概念，假設(shè)你有一個同時裝有氧氣和氮氣的盒子，彼此之間沒有隔板阻礙，理應(yīng)保持混合。

而此時也許會有一個叫做麥克斯韋妖的微觀惡魔，促使每次氧氣和氮氣原子碰撞時，會以某種方式反彈，讓氧氣全都飄到一側(cè)，而氮氣流向另一側(cè)。

這是一種統(tǒng)計學(xué)上的不可能構(gòu)型，但在數(shù)學(xué)上經(jīng)常發(fā)生。

例如圓周率π的位數(shù) 3.14159……。這些數(shù)字看似沒有規(guī)律，實則從長遠看，能看到和4、5、6一樣多的1、2、3，理論上不應(yīng)當偏向某一個數(shù)字，但也許π中也存在一個惡魔，當你計算越多位數(shù)時，它都會偏向某個數(shù)字，但我們目前的技術(shù)無法證明。

所以回到納維-斯托克斯問題，流體具有一定的能量，并且因為流體在運動，能量會被四處傳遞，同時水具有粘性，如果能量分散在許多不同的位置，流體的自然粘性就會使能量衰減并趨于零。

這在我們實際用水做實驗時常會發(fā)生，比如潑水時出現(xiàn)的湍流或波浪，最終會穩(wěn)定下來，振幅越低，速度越小，就越平靜。

但也許存在某種惡魔，它不斷地將流體的能量推向越來越小的規(guī)模，移動速度越來越快，在更快的速度下，粘度影響較小。

因此它可能會創(chuàng)造一種所謂的自相似爆破場景，其中流體的能量從某個大尺度開始，都轉(zhuǎn)移至流體中的一個較小區(qū)域，然后以更快的速度移動到更小的區(qū)域，依此類推。

每次花費的時間可能是前一次時間的一半，然后可以在有限時間內(nèi)收斂到集中于一點上的所有能量，即有限時間爆破。

所以如果你有一個大的水漩渦，它往往會分裂成更小的漩渦，但它不會把所有的能量從一個大漩渦全部轉(zhuǎn)移到某一個小漩渦，而是分散轉(zhuǎn)移到三四個小漩渦，小漩渦再各自分裂成三四個更小的漩渦。能量被分散到粘性可以控制一切的程度。

但如果能以某種方式集中所有能量，并且做得足夠快，以至于粘性效應(yīng)沒有足夠的時間來平息一切，那么爆炸就會發(fā)生。

所以有些論文聲稱，只需要考慮能量守恒，并小心使用粘性，你就可以控制納維-斯托克斯方程，甚至還可以控制許多類似類型的方程。

所以過去人們多次嘗試獲得納維-斯托克斯的全局正則性，這與有限時間爆炸相反，速度需要保持平滑，但所有嘗試都失敗了，總是存在一些無法挽救的符號錯誤或其它錯誤。

所以我感興趣的是，為什么我們無法證偽有限時間爆破。如果能平均納維-斯托克斯運動方程，那么我就能關(guān)閉某些水的相互作用方式，只保留部分需要的。

特別是如果有一個流體，它可以將能量從一個大渦流轉(zhuǎn)移到小渦流，我會關(guān)閉將能量轉(zhuǎn)移到其它漩渦的通道，而只引導(dǎo)它進入該小漩渦，同時仍然保持能量守恒定律。

我希望通過改變物理規(guī)律來制造爆炸，這是數(shù)學(xué)家可以做到的事情。

但也存在數(shù)學(xué)障礙，所以我做的工作是，當關(guān)閉方程的某些部分，它的非線性程度會降低，也會更趨向規(guī)則，不太容易爆炸。但我也發(fā)現(xiàn)，通過關(guān)閉一組精心設(shè)計的相互作用，我可以迫使所有能量在有限時間內(nèi)完成爆炸。

這意味著，如果想要證明納維-斯托克斯方程的全局正則性，必須利用真實方程所具有的某些特征，而這些特征是我的人工方程所無法滿足的。因此某些方法得以排除。

所以數(shù)學(xué)的關(guān)鍵在于，它不僅僅是找到一個有效的技術(shù)并應(yīng)用它，而是你需要避開那些無效的技術(shù)。對于真正困難的問題，通常有幾十種你可能認為適用的方法，但只有在積累了大量經(jīng)驗后，你才能意識到這些方法根本行不通。

所以為鄰近問題尋找反例，就可以排除掉它，從而節(jié)約時間，不會將精力浪費在根本不可能成功的事情上。

我的技術(shù)利用的就是超臨界性。在偏微分方程中，方程之間就像不同力量在拔河。而在納維-斯托克斯方程中，有兩個相互競爭的項：耗散項和傳輸項。如果來自粘性的耗散項占主導(dǎo)，那么你會得到正則性。如果傳輸項占主導(dǎo)，這將是一個不可預(yù)測的非線性情況。

但這些力在小尺度上保持平衡，但在大尺度上不平衡。納維-斯托克斯方程就是超臨界方程。在越來越小的尺度上，傳輸項比耗散項強得多，所以粘性使事物平靜下來。

這就是為什么在二維中問題很棘手，蘇聯(lián)數(shù)學(xué)家Ladyshenskaya在60年代就證明了在二維中沒有爆炸，納維-斯托克斯方程在二維是臨界的，即使在非常小的尺度上，傳遞效應(yīng)和粘性效應(yīng)的強度始終大致相同。

我們目前有很多技術(shù)來處理臨界和次臨界方程，并證明其正則性，但對于超臨界方程，情況尚不清楚。我對此做了很多工作，也有很多后續(xù)研究表明，對于許多其他類型的超臨界方程，你可以構(gòu)造出各種各樣的爆炸示例。

一旦非線性效應(yīng)在小尺度上主導(dǎo)了線性效應(yīng)，各種壞事都可能發(fā)生。所以超臨界性與臨界性和次臨界性會造成了很大的差異。

這是一個關(guān)鍵的定性特征，它區(qū)分出一些好的、可預(yù)測的方程，比如某些方程可以預(yù)測數(shù)百萬年或者至少數(shù)千年的行星運動。但我們無法將天氣預(yù)測到未來兩周以上，因為這是一個超臨界方程。因此方程在精細尺度上的非線性非常有趣。

而對于解決納維-斯托克斯方程，有一種天真的方法，就是不斷推動它進入下一個尺度，試圖強制讓其爆炸。事實證明，這在五維或更高維度中行得通。

但在三維中，我發(fā)現(xiàn)了一個有趣的現(xiàn)象，如果你改變物理定律，總是試圖將能量推入更小的尺度，能量雖然確實擴展出去了，但上一個尺度上仍然殘留有部分能量。結(jié)果這使它更容易受到粘性的影響，因此這種直接推進是不可行的。

所以我需要編程一個類似于氣閘的延遲，讓它在能量推入下一個尺度前一直停留，直到所有能量都被傳遞到該尺度上，才會開啟進入下一個更小尺度的閘門。這樣能量就可以逐級推進，抵抗粘性的影響。

當然這需要構(gòu)造一個相當復(fù)雜的非線性項，類似電子電路，利用電阻器和電容器的堆疊，創(chuàng)造一個門，然后利用時鐘建立閾值。這類似于魯布·戈德堡機械，卻是用數(shù)學(xué)描述的，這最終奏效了。

我意識到，也許能在實際方程中完成同樣的事情，例如將水的方程式想象成一種蒸汽朋克的東西。類比現(xiàn)代計算機由電子通過非常細小的電線，并與其他電子相互作用實現(xiàn)驅(qū)動。

想象水脈沖也以特定速度移動，可能存在兩種不同的構(gòu)型，分別對應(yīng)開或關(guān)。如果讓兩個運動水體碰撞，它會產(chǎn)生新的構(gòu)型，比如“與門”或“或門”，這樣輸出將以一種可預(yù)測的方式依賴于輸入。

將它們鏈接起來，也許能創(chuàng)造一臺圖靈機，一臺完全由水制成的計算機。接下來就可以做機器人技術(shù)，比如液壓等。可以創(chuàng)造一些流體模擬的機器，即馮·諾依曼機。

根據(jù)馮·諾依曼移民火星的提議，僅僅光機器運送人力的成本就高得離譜。但如果能運送一臺機器到火星，它可以自行開采火星材料并冶煉新機器，那么移民是可行的。

也就是建造一個流體機器，在某種寒冷狀態(tài)下可以創(chuàng)建自身的更小版本。大的水態(tài)機器人會將所有能量轉(zhuǎn)移到更小的構(gòu)型，然后關(guān)機進行自我清理。然后新構(gòu)型，它會啟動并做相同的事情，但更小更快。

而方程具有一定的縮放對稱性，可以實現(xiàn)不斷迭代。但實際上會讓納維-斯托克斯方程創(chuàng)造一個爆炸。

但現(xiàn)在這只是一個空想，因為有太多缺失的東西使它無法成為現(xiàn)實，例如無法創(chuàng)造基本的邏輯門、沒有特殊的水構(gòu)型、模擬計算總是存在錯誤、如何關(guān)閉大機器的電源而不干擾小機器的寫入等等。

它不違背任何物理定律，所以原則上一切都可以發(fā)生。當然現(xiàn)在也有其他小組正在追求使納維-斯托克斯爆炸的方法，他們實際上正在追求更接近直接自相似模型的東西，可以不完全按原樣工作，也可能存在有比我剛才描述的更簡單的方案來實現(xiàn)它。

生命游戲是一個離散方程

陶哲軒：數(shù)學(xué)的關(guān)鍵在于，它非常擅長發(fā)現(xiàn)一些完全不同的問題之間的聯(lián)系。只要數(shù)學(xué)形式相同，就能建立聯(lián)系。所以以前有很多關(guān)于元胞自動機的工作，其中最著名的是康威生命游戲。

存在一個無限的離散網(wǎng)格，在任何給定時間內(nèi)，網(wǎng)格要么被一個細胞占據(jù)，要么是空的，并且有一個非常簡單的規(guī)則，會告訴你這些細胞如何演化。所以，有時候細胞是存活的，有時候它們是死亡的。

這曾是一個非常流行的屏幕保護程序，實際上就是持續(xù)播放這些動畫，它們彼此之間相當混亂，甚至有時看起來會像湍流。

但在某個時刻，人們在這個生命游戲中發(fā)現(xiàn)了越來越多有趣的結(jié)構(gòu)，例如滑翔機。滑翔機是一個由四五個細胞組成的微小構(gòu)型，它會像漩渦環(huán)一樣朝著某個方向進化。

當然這是一個類比，生命游戲是一個離散方程，而納維-斯托克斯則是一個連續(xù)方程，但在數(shù)學(xué)上它們存在相似的特征。所以隨著時間的推移，可以在生命游戲中構(gòu)建更多有趣的東西。

它是一個非常簡單的系統(tǒng)。只需要大約三四個規(guī)則就可以實現(xiàn)。再比如有個叫滑翔機槍的東西，它除了吐出一個接一個的滑翔機之外，什么都不做。然后經(jīng)過科學(xué)家的大量努力，終于設(shè)法為滑翔機構(gòu)建了“與門”和“或門”。

這將是一個巨大的荒謬結(jié)構(gòu)，即如果有一串滑翔機流入，另一串滑翔機也流入，那么也許將會有一串新生成的滑翔機流出。但如果只有其中一串含有滑翔機，則不會有輸出。

所以一旦你可以構(gòu)建這些基本門，那么僅僅通過軟件工程，你就幾乎可以構(gòu)建任何東西，甚至一臺巨大的蒸汽朋克類型的圖靈機。

后來人們也確實在生命游戲中生成了可自我復(fù)制的巨大機器，一臺馮·諾依曼機器，在很長一段時間內(nèi)，人們認為它的內(nèi)部就像滑翔機槍在完成計算，因為它會自我創(chuàng)建另一個可以復(fù)制的自己。

實際上，這其中很多工作都是由業(yè)余數(shù)學(xué)家們一起完成的。這也是啟發(fā)我提出在納維-斯托克斯方程中做同樣事情的部分原因。

當然，模擬要比數(shù)字差得多，不能直接把生命游戲中的構(gòu)造放進去。但它也再次說明，這是存在可能性的。

Lex Fridman：細胞自動機中會發(fā)生類似于流體的涌現(xiàn)，大規(guī)模運作的局部規(guī)則可以創(chuàng)造出極其復(fù)雜的動態(tài)結(jié)構(gòu)。那么其中有任何部分適合進行數(shù)學(xué)分析的嗎？或者是否存在工具加以解釋。

陶哲軒： 問題是，只有通過非常精心準備的初始條件，才能獲得這種涌現(xiàn)的復(fù)雜結(jié)構(gòu)。對于滑翔機槍、門和自推進機器，如果只是隨機放置細胞，那么將不會出現(xiàn)此類結(jié)構(gòu)。

這與納維-斯托克斯方程的情況類似，在典型的初始條件下，不會進行任何奇怪的計算。但通過工程或者以非常特殊的方式專門設(shè)計，就可以做出足夠聰明的構(gòu)造。

這在數(shù)學(xué)中是一個反復(fù)出現(xiàn)的挑戰(zhàn)，可以稱之為結(jié)構(gòu)與隨機性之間的二分法，即數(shù)學(xué)中的大多數(shù)生成對象都是隨機的，只有極少數(shù)事物存在固定模式。

但現(xiàn)在，我們可以通過構(gòu)造來證明某物存在模式，只要能夠證明它確實每隔一段時間就會重復(fù)自己一次。例如，你可以證明大多數(shù)數(shù)字序列都沒有模式。只要隨機選取數(shù)字，就會出現(xiàn)大數(shù)定律，它會說明，從長遠來看，你會得到和2一樣多的1。

但如果給定一個特殊模式，比如π的數(shù)字，該如何證明它沒有某種奇怪的模式呢？于是我花了很多時間，做的另一項工作是證明所謂的結(jié)構(gòu)定理或逆定理，這些定理將會為事物何時可以變得非常結(jié)構(gòu)化而提供檢驗。

有些函數(shù)是含有加性的，比如你有一個自然數(shù)映射函數(shù)，可以將2映射到4，3映射到6等。函數(shù)的加性意味著如果把兩個輸入疊加，輸出也會相加，例如如果你把a+b乘以10，就等同于把a乘以10和把b乘以10然后相加。

但有些函數(shù)并不是完全可加的，例如取數(shù)n為10，乘以√2，然后取整，結(jié)果約為14點幾，取整到14。n為20時則算下來取整到28。此時加性成立，10+10得20，14+14得28。

這種取整方式有時也會存在舍入誤差，當把a+b相加時，函數(shù)給出的結(jié)果并不完全等于兩個單獨輸出的和，而是和加上或減去一。所以此時它幾乎是加性的但又不完全加性。

因此我在這上面做了很多工作，大致是如果一個函數(shù)表現(xiàn)出類似結(jié)構(gòu)，那么基本上是有原因的，即附近存在一些其他函數(shù)。而它自己實際上是完全結(jié)構(gòu)化的。

所以如果你能明確出逆定理，就會創(chuàng)造出二分法，即要么該研究對象完全沒有結(jié)構(gòu)，要么它們以某種方式與結(jié)構(gòu)化的東西相關(guān)。但無論是哪一種情況，你都可以取得進展。

無限：假設(shè)是球形的奶牛

陶哲軒：一個很好的例子是數(shù)學(xué)中的塞邁雷迪定理，于1970年代得以證明，它涉及在一組數(shù)字集合中尋找某種類型的模式，即等差數(shù)列，例如3、5、7或10、15、20。

塞邁雷迪證明了，對于任何足夠大的數(shù)字集合，即正密度集合，都包含有任意長度的等差數(shù)列。例如，奇數(shù)集合的密度為1/2，則其中包含任意長度的等差數(shù)列，因為其實奇數(shù)集合相當結(jié)構(gòu)化，我可以輕松找到像11、13、15、17這個等差數(shù)列。

塞邁雷迪定理也同樣適用于隨機集合。如果我取一組奇數(shù)集合，然后拋擲一枚硬幣，只保留擲出正面的數(shù)字，隨機去掉一半的數(shù)，將得到一個完全沒有模式的集合。但由于隨機波動，你仍然會在這個集合中找到許多等差數(shù)列。

Q：能否證明在隨機集合中存在任意長度的等差數(shù)列？

陶哲軒： 可以的，比如說無限猴子定理。如果一個房間內(nèi)有無數(shù)會使用打字機的猴子，讓它們隨機打字，其中一只一定會打出完整的《哈姆雷特》劇本或任何其他有限的文本字符串。這需要相當長的時間，但只要是無限，那么它終會發(fā)生。

所以如果你取一個無限的數(shù)字串或其他，最終都會呈現(xiàn)出你想要的任何有限模式，只是需要很長時間，等差數(shù)列也是如此。

Q：人類應(yīng)當如何看待無限呢？

陶哲軒：可以把無限視作一個有限數(shù)的抽象，而它沒有界限。但現(xiàn)實生活中其實沒有真正的無限，但你可以假設(shè)，比如如果我想有多少錢就有多少錢，想走多快就可以走多快。

數(shù)學(xué)家就是利用數(shù)學(xué)將這種形式主義理想化，不是極大或極小，而是無限或零。此時，數(shù)學(xué)將變得簡潔。

在物理學(xué)中，我們常常開玩笑地說，假設(shè)是球形的奶牛，現(xiàn)實世界中的問題總會受現(xiàn)實世界影響，但你可以理想化，將某些東西送到無限，某些東西送到零，數(shù)學(xué)就變得容易處理。

Lex Fridman：我想知道使用無窮大有多頻繁地迫使我們偏離現(xiàn)實世界的物理規(guī)律。

陶哲軒：這里存在很多陷阱。我們在本科數(shù)學(xué)課上花費了很多時間教授分析學(xué)，但分析學(xué)是關(guān)于如何取極限，例如a+b恒等于b+a，有限項可以交換，但無限項時，如果有一個收斂于某值的級數(shù)，重新排列，它將突然收斂于另一個值，則會出現(xiàn)錯誤。

所以當使用無限時，必須引入ε和δ，以及特定的推理方式，以避免類似錯誤。

近年來，人們開始對無限極限下成立的結(jié)果進行有限化，也就是說，某件事最終將會成真，但無法確定具體時間和速率。

那么如果我沒有無限只猴子，而是有限只，我需要等待多久才能看到《哈姆雷特》出來呢？這是一個定量問題，可以用純粹有限的方法解決，或者利用你的有限直覺。

結(jié)果表明，生成的文本長度將呈指數(shù)級增長，這也就是為什么你永遠看不到猴子寫出《哈姆雷特》的原因。也許你能看到猴子們寫出了一個包含四個字母的單詞，但僅此而已。

所以我發(fā)現(xiàn)，當把一個無限的陳述有限化，它就會變得直觀得多，也就沒那么奇怪了。當然缺點是有限化群要混亂得多，而無限化群在幾十年前就得以發(fā)現(xiàn)，后來人們才將其有限化。

數(shù)學(xué)關(guān)注模型，物理解釋模型

Q：數(shù)學(xué)與物理學(xué)之間，在理解和看待世界的方式上有什么區(qū)別？

陶哲軒：我認為科學(xué)通常是三者之間的相互作用：現(xiàn)實世界、我們對現(xiàn)實世界的觀察，以及我們認為世界如何運作的心理模型。

我們無法直接接觸現(xiàn)實，我們只擁有不完整且存在很多誤差的觀測結(jié)果。當我們想要預(yù)測的時候，例如預(yù)測天氣，我們只有簡化的模型，有時也只能給出不切實際的假設(shè)，就像球形奶牛。

這就是數(shù)學(xué)模型，數(shù)學(xué)關(guān)注的是模型，而科學(xué)收集觀察結(jié)果并提出解釋模型。數(shù)學(xué)讓我們停留在模型內(nèi)部，并詢問模型帶來的后果，以及對未來會做出什么預(yù)測、是否符合過去的觀測數(shù)據(jù)。而這期間肯定存在共生關(guān)系。

數(shù)學(xué)與其他學(xué)科相比，是很不同尋常的，因為數(shù)學(xué)始于假設(shè)，比如模型的公理和模型的結(jié)論。但幾乎其它學(xué)科中，都是始于結(jié)論，比如我想建一座橋，然后去找到通往那個結(jié)果的路徑。這當中很少存在假設(shè)，當然推理小說除外。

我們生活中所做的絕大多數(shù)事情都是由結(jié)論驅(qū)動的，包括物理學(xué)和科學(xué)，例如“這顆小行星會去向哪里？”、“明天的天氣會是怎樣？”，但數(shù)學(xué)卻是從公理出發(fā)。

Q：物理學(xué)中存在理論與實驗之間的張力，你認為發(fā)現(xiàn)有關(guān)現(xiàn)實的真正新穎思想的強有力方法是什么？

陶哲軒：需要同時擁有自上而下和自下而上，這是所有事物之間真正的互動關(guān)系。隨著時間推移，觀察、理論和建模都應(yīng)該更接近現(xiàn)實，即使一開始它們總是相距甚遠，只需要擁有其中一個就能弄清楚將另一個推向何方。

因此，如果你的模型預(yù)測的是實驗未捕捉到的異常情況，它將會告訴實驗者去哪里查找更多數(shù)據(jù)來優(yōu)化模型，這需要反復(fù)操作。

在數(shù)學(xué)本身中，也存在理論和實驗的部分。只是最近，理論幾乎完全占據(jù)主導(dǎo)地位。99%的數(shù)學(xué)是理論數(shù)學(xué)，實驗數(shù)學(xué)非常少。因為假如他們想要研究素數(shù)或者其它，可以直接利用計算機生成大型數(shù)據(jù)集。

就像高斯發(fā)現(xiàn)了一個猜想，數(shù)論中最基本的素數(shù)定理，它預(yù)測了一百萬乃至一萬億可以有多少個素數(shù)。這個問題上，他主要靠自己計算，但也雇傭了人類計算員，用以計算前100000個素數(shù)并制作表格，做出預(yù)測。

這是實驗數(shù)學(xué)的一個早期例子，但顯然理論數(shù)學(xué)要成功得多，也是直到最近，做一些復(fù)雜的數(shù)學(xué)計算才變得可行。但即便我們現(xiàn)在擁有強大的計算機，也只有一部分數(shù)學(xué)事物可以通過數(shù)值探索。

比如有一種叫做組合爆炸的東西，當你想研究1到1000的所有可能子集，子集數(shù)量將會是2 的1000次方，這比目前的任何計算機可枚舉的都要大得多。所以有些數(shù)學(xué)問題無法直接通過暴力計算來解決。

國際象棋則是另一個著名的例子。關(guān)于國際象棋排列的數(shù)量，我們至今無法用計算機完全解決，但我們現(xiàn)在有AI，它們不會探索博弈樹中的每個位置，而是尋求近似值。

事實上人們現(xiàn)在就正在使用這種國際象棋引擎來做實驗性國際象棋。他們正在重新審視古老的國際象棋理論，例如傳統(tǒng)的經(jīng)典開局，也許并不是最優(yōu)解，他們希望用國際象棋引擎來實現(xiàn)改進。

我希望數(shù)學(xué)在未來會有更大的實驗成分，也許將由AI驅(qū)動。

數(shù)學(xué)的不合理但有效

Lex Fridman：你提到了柏拉圖的洞穴寓言。如果人們不知道洞穴是人們觀察現(xiàn)實的影子，而不是現(xiàn)實本身，并且他們相信他們所觀察到的就是現(xiàn)實——從某種意義上說，這是數(shù)學(xué)家和也許所有人類都在做的事情，即觀察現(xiàn)實的影子——我們有可能真正接觸到現(xiàn)實嗎？

陶哲軒：這當中存在三個本體論的東西，分別是實際的現(xiàn)實、我們的觀察和我們的模型，嚴格來說它們彼此不同，而我認為它們將永遠不同。但它們會隨著時間逐漸靠近，但在靠近的過程中必須舍棄掉你最初的直覺。

例如在天文學(xué)中，最初人們認為世界模型是平的，因為它看起來很平，且很大。而宇宙的其余部分，即天空，則看起來很小。所以當你從模型出發(fā)，它實際上與現(xiàn)實相去甚遠，但它又符合當下你的觀察結(jié)論。

但隨著時間推移和越來越多的觀察，模型將更接近現(xiàn)實，我們也會意識到地球是圓的，它在旋轉(zhuǎn)，并圍繞著太陽系運行，而太陽系圍繞著銀河系運行，而宇宙在膨脹，膨脹本身也在加速膨脹……但事實上就在今年，我們發(fā)現(xiàn)宇宙的加速也是非恒定的，由于暗物質(zhì)或暗能量這類東西的存在。

我們有一個數(shù)據(jù)擬合相當好的模型，在某種程度上可以解釋它。該模型只有幾個你必須指定的參數(shù)。但人們會說，那是捏造因子，有足夠的捏造因子，你就可以解釋任何事情。可是數(shù)學(xué)的觀點是，希望模型中的參數(shù)要比觀測數(shù)據(jù)集中的數(shù)據(jù)點少。

如果一個模型有10個參數(shù)，可以解釋10個觀測結(jié)果，該模型將完全無用，這叫做過擬合。而如果你的模型只有兩個參數(shù)，卻解釋了1萬億個觀測結(jié)果，這就是暗物質(zhì)模型，我認為它有14個參數(shù)，可以解決天文學(xué)家擁有的PB級數(shù)據(jù)。

所以你可以把一個物理數(shù)學(xué)理論看作是對宇宙的一種數(shù)據(jù)壓縮，即把這些PB級數(shù)據(jù)壓縮為一個可以用五頁紙描述的模型，并指定一定數(shù)量的參數(shù)，如果它能以合理的精度擬合幾乎所有的觀測結(jié)果，那么壓縮越多，你的理論就越好。

愛因斯坦說過這樣一句話：“宇宙中最難以理解的事情是它是可理解的。”，這就是數(shù)學(xué)的不合理但有效。

實際上這里有一些可能的數(shù)學(xué)解釋，比如數(shù)學(xué)中有一種叫做普適性的現(xiàn)象。許多宏觀尺度上的復(fù)雜系統(tǒng)都是從大量微觀尺度上的微小相互作用中產(chǎn)生，而由于組合爆炸，你會認為宏觀尺度的方程一定比微觀尺度的方程指數(shù)級復(fù)雜。

如果要完全精確地求解，比如模擬一盒空氣中的所有原子，就像阿伏伽德羅常數(shù)這將會是巨大的，如果你真的試圖跟蹤每一個粒子，這將是荒謬的。

但某些定律只在微觀尺度上涌現(xiàn)，幾乎不依賴于宏觀尺度上發(fā)生的事情，或者只依賴于非常少的幾個參數(shù)。所以，如果要模擬盒子里包含萬億粒子的氣體，只需要知道它的溫度、壓力、體積以及五六個參數(shù)，就可以模擬10^23或任何數(shù)量的粒子的所有信息。

因此，我們無法在數(shù)學(xué)上理解普適性，但存在一些可以幫助我們理解普適性發(fā)生原因的玩具模型，例如中心極限定理就解釋了為什么鐘形曲線在自然界中無處不在，那么多事物都是高斯分布。

現(xiàn)在甚至還有一個攜帶鐘形曲線的模因，甚至模因也具有普適性。如果你愿意，你可以選擇元，但存在許多過程，比如選取很多獨立的隨機變量，以各種方式將它們平均在一起，取簡單平均或更復(fù)雜的平均，我們就可以在各種情況下證明高斯曲線的出現(xiàn)。

但如果你有許多不同的輸入，且它們之間存在某種系統(tǒng)關(guān)聯(lián)，則可能得不到鐘形曲線，所以普適性并不是100%可靠。

全球金融危機就是這方面的一個著名例子。人們認為抵押貸款違約的行為存在高斯曲線，如果在擁有抵押貸款的十萬美國人中，詢問違約比例，如果一切都是去相關(guān)的，將會生成漂亮的鐘形曲線，然后你可以用期權(quán)和衍生品管理風險。

但如果經(jīng)濟中存在系統(tǒng)性沖擊，推動所有人同時違約，那將是非常反高斯的行為，這就是2008年沒有被充分考慮進去的后果。

我認為，現(xiàn)在人們更多地意識到，系統(tǒng)性風險實際上是一個更大的問題，模型很漂亮，但它可能不匹配現(xiàn)實。所以研究模型行為的數(shù)學(xué)非常重要，但也需要科學(xué)來驗證它何時符合現(xiàn)實，何時不符合。兩者都被需要。

而數(shù)學(xué)可以提供幫助，因為像中心極限定理就會告訴你，某些假設(shè)的輸入之間如果不相關(guān)，那么你就會擁有高斯行為。它也會告訴你到哪里去尋找模型中的弱點。

所以如果你理解中心極限定理，就可以使用高斯行為或其它來模擬違約風險，如果你受過數(shù)學(xué)訓(xùn)練，你就會尋求輸入之間的系統(tǒng)相關(guān)性，并詢問經(jīng)濟學(xué)家這樣存在多大的風險，然后你就可以繼續(xù)了。所以在科學(xué)和數(shù)學(xué)之間總是存在這種協(xié)同作用。

Q：是否存在一種可以將不同領(lǐng)域的數(shù)學(xué)連接起來的底層結(jié)構(gòu)？

陶哲軒：肯定存在相互聯(lián)系的線索，數(shù)學(xué)的很多進展都來自于將兩個先前沒有聯(lián)系的數(shù)學(xué)領(lǐng)域聯(lián)系起來。一個古老的例子是幾何和數(shù)論。在古希臘時代，它們并不被認為是相關(guān)的，直到笛卡爾意識到并發(fā)展了解析幾何，可以用兩個實數(shù)來參數(shù)化幾何對象平面。幾何問題最終可以轉(zhuǎn)化為數(shù)字問題。

當然今天這兩個領(lǐng)域已經(jīng)統(tǒng)一了，類似的過程也在數(shù)學(xué)中反復(fù)上演，代數(shù)和幾何曾是分開的，現(xiàn)在又有了代數(shù)幾何。

我認為數(shù)學(xué)家也有各種風格，就像刺猬和狐貍，狐貍知道很多事但都只懂一點，而刺猬只知道一件事但知道得很深。理想的數(shù)學(xué)家合作就需要多樣性，讓一只狐貍與多只刺猬合作，或者反之亦然。

我主要認為自己是一只狐貍，我很喜歡套利這個金融說法，學(xué)習一個領(lǐng)域是如何運作的，了解該領(lǐng)域的技巧，然后去到另一個不相關(guān)領(lǐng)域，但我可以自行調(diào)整這些技巧，看到領(lǐng)域之間的聯(lián)系。

所以還存在許多比我研究更深的科學(xué)家，他們是真的刺猬，了解一個領(lǐng)域的一切，且在那個領(lǐng)域更快、更有效，而我可以給他們提供額外的工具。

而兩種思考之間，我更傾向成為狐貍，我喜歡尋找類比、敘述。假如我看到一個領(lǐng)域的結(jié)果并且很喜歡，但我不喜歡證明，尤其是它使用了我不是很熟悉的數(shù)學(xué)類型，我將經(jīng)常會嘗試用我喜歡的工具重新證明它。

通常我的證明更糟糕，但通過這樣練習，我可以充分明白另一個證明試圖在做些什么。由此我可以對那個領(lǐng)域使用的工具有所理解。這是非常具有探索性的，非常像是在瘋狂的領(lǐng)域里做瘋狂的事情，并且像是在大量重新發(fā)明輪子。

刺猬風格也會更學(xué)術(shù)，你將會非常注重知識，及時了解這個領(lǐng)域的所有進展。了解所有歷史并對每種特定技術(shù)的優(yōu)缺點有很好的理解。你會更依賴計算而不是試圖尋找敘述。當然我也可以那樣做，但始終有其他人在那方面更為擅長。

Q：你是在什么時候意識到數(shù)學(xué)可以有一種優(yōu)雅和美感的？

陶哲軒：當我來到普林斯頓讀研究生時，John Conway當時也在那里，他于幾年前去世了。但我記得我參加的最早的研究講座之一，就是Conway關(guān)于他的極端證明的報告。

Conway會以一種你通常不會想到的方式思考各種事物，他認為證明本身就占據(jù)了某種空間，所以如果你想證明某件事，比如說有無限多個素數(shù)，你可以把它們放到不同的軸上。

有些證明是優(yōu)雅的，有些證明很長，有些證明是初級的。這樣就有了證明空間，且空間本身具有某種形狀。他對形狀的極值點很感興趣，比如在所有證明中，什么是以犧牲其他一切為代價的最短證明？或者什么是最初等的證明？或者其它。

所以他列舉了一些著名定理的例子，然后他會給出他認為是這些定理的極端證明。這真的讓人大開眼界，這不僅是得到一個有趣的結(jié)果證明，而且一旦你有了這個證明，試圖用各種方式優(yōu)化它，證明本身就擁有了一些技巧。

這也影響了我的寫作風格。比如當你做本科數(shù)學(xué)作業(yè)時，你被鼓勵寫下任何有效的證明并交上去，得到一個勾，你就繼續(xù)前進。

但如果你希望你的結(jié)果真正具有影響力并被人們閱讀，它就不能只是正確的。它也應(yīng)該讓閱讀成為一種享受，才能有動力推廣到其他事物。

這和許多其他學(xué)科一樣，比如像編碼。數(shù)學(xué)和編碼之間有很多類比。就像你可以用意大利面條式代碼編寫一些東西，它適用于某個任務(wù)，又快又臟而且高效。但其實有很多可以寫好代碼的好原則，這樣其他人就可以使用它，并在此基礎(chǔ)上構(gòu)建，減少錯誤的發(fā)生，數(shù)學(xué)也有類似的事情。

另外還有一種叫做代碼高爾夫的活動，我也覺得它美麗而有趣。人們使用不同的編程語言，來試圖寫出完成特定任務(wù)的最短程序。我甚至相信這里存在一個比賽，不僅可以對程序進行壓力測試，還可以對證明或者不同語言進行測試。也許這是一種不同的符號，用以完成不同的任務(wù)。

Lex Fridman：你覺得數(shù)學(xué)中最美麗或最優(yōu)雅的方程是什么？歐拉恒等式常被認為是數(shù)學(xué)中最美麗的方程，你是否在那個方程式中，在歐拉恒等式中找到了美？

陶哲軒：我來說的話，我覺得最吸引人的是不同事物之間的聯(lián)系，歐拉恒等式使用了所有的基本常數(shù)，這很可愛。但對我來說，指數(shù)函數(shù)是歐拉引入來測量指數(shù)增長的，所以復(fù)利或衰減，任何持續(xù)增長、持續(xù)減少、膨脹或收縮的東西，都可以用指數(shù)函數(shù)建模。

而π來自圓和旋轉(zhuǎn)，如果你想轉(zhuǎn)一根針180度，你需要旋轉(zhuǎn)π弧度。而i復(fù)數(shù)表示虛軸上的擺動，對應(yīng)90度的旋轉(zhuǎn)，所以是方向上的改變。所以指數(shù)函數(shù)代表當前方向上的增長和衰減。當你在指數(shù)中加入i時，它現(xiàn)在變成與當前位置成直角的運動。

然后歐拉恒等式將告訴你，如果你旋轉(zhuǎn)一個時間π，你最終會得到另一個方向。它將通過復(fù)化和i的旋轉(zhuǎn)，將所有數(shù)學(xué)工具統(tǒng)一起來，包含數(shù)學(xué)、動力學(xué)、幾何和復(fù)數(shù)。

而當你第一次研究任何東西時，你必須測量事物并為它們命名，有時因為模型與現(xiàn)實相去甚遠，也會給錯誤的東西起了好名字，但直到后來你才發(fā)現(xiàn)什么是真正重要的東西。

例如在物理學(xué)中，E=MC2，其中一件大事就是E，而當亞里士多德首次提出運動定律，然后是伽利略或牛頓能測量質(zhì)量、加速度、力等等，所以有了著名的牛頓第二運動定律F=ma。因為這些是主要對象，所以它們被賦予理論中的核心位置。

直到后來人們開始分析這些方程，才發(fā)現(xiàn)似乎這些量總是守恒的，特別是動量和能量。而事物是否擁有能量，這并不明顯，能量它不像質(zhì)量、速度那樣可以直接測量，但隨著時間推移，人們逐漸意識到這實際上是一個非常基本的概念。

哈密頓最終在19世紀將牛頓物理定律重新表述為哈密頓力學(xué)，其中能量，也就是哈密頓量是主導(dǎo)對象，一旦你知道如何測量任何系統(tǒng)的哈密頓量，你就能完全描述動力學(xué)，即所有狀態(tài)會發(fā)生什么。

它作為核心角色，起初也并不明顯，而當量子力學(xué)出現(xiàn)時，視角的轉(zhuǎn)變則提供了很大的幫助。研究量子力學(xué)的早期物理學(xué)家，他們首先嘗試將牛頓力學(xué)融入量子力學(xué)，但遇到了很多麻煩，因為一切都是粒子，而我認為它是波，總之結(jié)合起來非常奇怪。

如果你問，F(xiàn)=ma的量子版本是什么，這很難回答。但事實證明，在經(jīng)典力學(xué)背后的哈密頓量也是量子力學(xué)的關(guān)鍵對象，這里也有一個叫做哈密頓算符的對象。它是一種不同類型的對象，是運算符而不是函數(shù)，但一旦指定了它，你就指定了整個動力學(xué)。

所以這里有一個叫做薛定諤方程的東西，它可以準確地告訴你，一旦你擁有哈密頓量，量子系統(tǒng)將會如何演變。

所以將二者放在一起，看起來是完全不同的對象，一個涉及粒子，一個涉及波。但有了中心性，就可以將很多直覺和事實從經(jīng)典力學(xué)轉(zhuǎn)移到量子力學(xué)。

例如，在經(jīng)典力學(xué)中，有一個叫做諾特定理的東西。每當物理系統(tǒng)中存在對稱性，就有出現(xiàn)守恒定律。所以物理定律是平移不變的。

比如如果我向左移動10步，我會體驗到與初始位置相同的物理定律，這對應(yīng)動量守恒。而如果我以某個角度轉(zhuǎn)身，我又將再次體驗到相同的物理定律。這對應(yīng)角動量守恒。如果我等待10分鐘，我仍然有相同的物理定律，由于存在時間平移不變性，這對應(yīng)能量守恒定律。

所以在對稱性和守恒之間存在這種基本聯(lián)系，這在量子力學(xué)中也成立。盡管方程完全不同，但因為它們都源于哈密頓量，哈密頓量控制一切。當每次哈密頓量具有對稱性時，方程就會有一個守恒定律。所以一旦你擁有正確的表述，很多事情都變得清晰起來。

我們無法統(tǒng)一量子力學(xué)和廣義相對論，因為我們還沒有弄清楚基本對象是什么，例如我們必須放棄空間和時間的概念，因為這些空間幾乎是歐幾里得類型，只在非常小的尺度上出現(xiàn)量子漲落，從而形成時空泡沫，試圖用笛卡爾坐標xyz解釋是行不通的，但我們還不知道用什么來代替它。我們沒有類似于哈密頓量能組織起一切的類似數(shù)學(xué)概念。

直覺就在那里，你必須轉(zhuǎn)移它

Q：你的直覺是否認為存在一個萬物理論，可以找到一個統(tǒng)一廣義相對論和量子力學(xué)的語言？

陶哲軒：我相信如此。多年來，物理學(xué)的歷史就是統(tǒng)一的歷史，就像數(shù)學(xué)一樣。例如電和磁是分開的理論，然后麥克斯韋統(tǒng)一了它們。牛頓統(tǒng)一了天體的運動與地球上物體的運動。等等諸如此類，都說明了統(tǒng)一時有發(fā)生。

再次回到這個觀察和理論的模型，我們物理學(xué)的兩個大理論，廣義相對論和量子力學(xué)，現(xiàn)在發(fā)展如此之好，加起來涵蓋了我們所能做的所有觀察的99.9%。

你現(xiàn)在要么去研究極其瘋狂的粒子加速器，或者早期宇宙，再或者那些知道很難以測量的東西，才能偏離這兩個理論中的任何一個，直到你真正弄清楚二者如何結(jié)合在一起。

但我相信，我們已經(jīng)這樣做了幾個世紀，我們在以前也已取得一定進展，沒理由我們應(yīng)該放棄。

Q：您認為您會成為一名發(fā)展萬物理論的數(shù)學(xué)家嗎？

陶哲軒：經(jīng)常發(fā)生的情況是，當物理學(xué)家需要一些數(shù)學(xué)理論時，通常數(shù)學(xué)家們已經(jīng)研究出了一些前身理論。

所以當愛因斯坦開始意識到空間是彎曲的，他去找一些數(shù)學(xué)家詢問彎曲空間理論是否可用，然后他說，他認為黎曼發(fā)展了黎曼幾何學(xué)，這恰恰是一種空間以各種一般方式彎曲的理論。事實證明，這就是愛因斯坦理論幾乎完全需要的。

這就又回到了數(shù)學(xué)的不合理的有效性，那些能很好地解釋宇宙的理論，往往也能很好解決具有相同數(shù)學(xué)對象的數(shù)學(xué)問題。歸根結(jié)底，它們只是組織數(shù)據(jù)的兩種有效方式。

而弦理論，雖然幾十年來一直保持領(lǐng)先，但我認為它正在慢慢退出歷史舞臺，因為它與實驗并不匹配。

Lex Fridman：當前最大的挑戰(zhàn)之一就是實驗非常困難，因為兩種理論都如此有效，但另一方面，你所談?wù)摰牟粌H是偏離時空，更是進入一些瘋狂的維度，你現(xiàn)在所做的事情，對我們來說，已經(jīng)距離我們認為地球是平坦的時候相隔甚遠，我們很難用有限的認知來感知那個所謂的現(xiàn)實到底是什么。

陶哲軒：這就是為什么類比如此重要。圓形的地球并不直觀，因為我們被困在其上，但我們對圓形物體以及光的工作原理有相當好的直覺。

實際上，這是一個很好的練習，為了真正弄清楚日食、月相是如何發(fā)生的，可以用圓形地球、圓形月亮的模型很輕松地解釋。你可以拿一個籃球、一個高爾夫球和一個光源，自己實際去做這些事情，直覺就在那里，你必須轉(zhuǎn)移它。

現(xiàn)代科學(xué)也許是自身成功的受害者，為了更加準確，需要離最初的直覺越來越遠。因此，對于沒有經(jīng)歷過科學(xué)教育的人來說，這個過程顯得相當可疑，因此我們需要更多科學(xué)基礎(chǔ)。

有些科學(xué)家做了相當出色的外出推廣工作，但在家里也可以做很多科學(xué)的事情。YouTube上有很多視頻，我最近就和Grant Sanderson一起做了一個YouTube視頻，我們討論古希臘人如何能夠測量到月球的距離、到地球的距離，并使用你自己也可以復(fù)制的技術(shù)，不一定是花哨的太空望遠鏡或令人生畏的數(shù)學(xué)。

改變視角真的很重要。旅游可以拓寬思維，而這就是智力旅行，你把自己放在古希臘人或者其它時期的人的腦海中，做出球形奶牛的假設(shè)，這是數(shù)學(xué)家所做的，也是一些其他藝術(shù)家正在做的。

如果你提出公理，那么數(shù)學(xué)會讓你遵循這些公理并得出結(jié)論，有時你將可以從初始假設(shè)中走得很遠。

想象自己是個矢量場

Q：能否從數(shù)學(xué)的角度解讀廣義相對論，它的那一方面讓你感興趣，對你來說具有挑戰(zhàn)性？

陶哲軒：我研究過一些方程。有一個叫做波映射方程或西格瑪場模型的東西，它并不完全等同于時空引力本身的方程，而是某些可能存在于時空之上的場的方程。

所以愛因斯坦的相對論方程只描述時間和空間本身，但還有其他場存在，比如電磁場、楊-米爾斯場，以及一整套不同的方程。

其中愛因斯坦方程被認為是最非線性和困難的方程之一，但在層次結(jié)構(gòu)中相對較低的，是這個叫做波映射方程的東西。

這是一個波，在任意給定點上都像是被固定在一個球體上。所以我可以想象時空中有許多箭頭，這些箭頭指向不同的方向，像波浪一樣傳播。如果你擺動其中一個箭頭，它會傳播并使所有箭頭移動，這有點像麥田里的麥浪。

我對這個方程的全局正則性問題很感興趣，那么是否可以讓所有能量集中于一點呢？所以我考慮的方程實際上是所謂的臨界方程，它實際上在所有尺度上的行為都大致相同。我勉強證明了，你實際上無法強迫所有能量都集中到一點上，能量必須在此刻稍微分散一點，而一旦它分散一點點，它就會保持正則。

是的，這是在2000年發(fā)生的事。所以這其實也是我后來對納維-斯托克斯方程感興趣的部分原因。我開發(fā)了一些技術(shù)來解決這個問題，所以得出的部分結(jié)論是由于球體的曲率，這個問題實際上是非線性的，存在一種非微擾效應(yīng)。

當你正常觀察它時，它看起來比波動方程的線性效應(yīng)更大，即使你的能量很小，也很難將其控制。

但我開發(fā)了一種叫做規(guī)范變換的東西，方程有點像麥浪的演化，它們都在來回彎曲，存在很多運動。但如果想象一下，通過在空間的不同點上，附加小攝像機來穩(wěn)定流動，這些攝像機試圖以捕捉大部分運動的方式移動，在這種穩(wěn)定的流動下，流動將會變得線性得多。

我發(fā)現(xiàn)了一種可以減少非線性效應(yīng)量的變換方程，然后我就能夠求解這個方程了。這是我在澳大利亞拜訪我的姨母時，發(fā)現(xiàn)的這個變換，當時我試圖理解所有這些場的動力學(xué)，但我無法單單用紙筆完成，也沒有足夠的計算機設(shè)備來做任何計算機模擬。

所以我最終閉上眼睛，躺在地板上，想象自己實際上是個矢量場，然后來回翻滾，試圖找到如何改變坐標，讓各個方向的事物都能以合理的線性方式運行。

當我這樣做時，我的姨母走進來問道，我在做什么。我回答說，這很復(fù)雜。于是姨母說，好吧，你是年輕人，我不多問了。

學(xué)會策略性“作弊”

Q：你是如何解決難題的，是否在腦海中經(jīng)常可視化數(shù)學(xué)對象、符號？

陶哲軒：有很多的紙和筆。作為一名數(shù)學(xué)家，我學(xué)到的一件事情是，策略性作弊。

數(shù)學(xué)之美在于你可以隨心所欲地改變規(guī)則、改變問題，這是其它任何領(lǐng)域都無法做到的一點。如果你是一名工程師，有人說，在這條河上建造一座橋，你不能說，我想在這里建一座橋或者我想要紙而不是鋼來建造它，但作為數(shù)學(xué)家，你可以做任何你想要做的事情。

這就像試圖通關(guān)一個電腦游戲，其中有無限的作弊碼可用。你可以自行設(shè)置，例如有一個很大的維度，我可以先將其設(shè)為一，先解決一維問題，因此存在一個主項和一個誤差項，所以我需要做一個球形奶牛假設(shè)，假設(shè)誤差項為零。

所以當你試圖尋找解決問題的方法，不應(yīng)該在鐵人模式下進行，讓事情變得最大化困難，更合理的解決方式是，如果有10件事讓你的生活變得困難，你可以先找到其中一個問題并關(guān)閉另外九個困難。

這樣你就安裝了九個作弊碼，而如果你安裝了十個作弊碼，那么這個游戲?qū)⑹俏⒉蛔愕赖摹．斈惆惭b九個，然后集中解決那一個問題，它將教會你如何解決那個特定的困難，然后你關(guān)閉這個，再打開其它問題并依次解決。在你最終學(xué)會如何分別解決這10個問題后，再將其中幾個合并處理。

小時候，我看了很多我們文化中的香港動作片，每次遇到打斗畫面，例如英雄會被一百個壞蛋嘍啰包圍，在精心設(shè)計的場景下，他一次只會與一個人戰(zhàn)斗，打敗那個人后再繼續(xù)前進。正因為如此，他可以打敗他們所有人。

但是，如果這群人更聰明一點，就應(yīng)該直接蜂擁而上，當然這樣電影效果會很糟糕，但他們會贏。

Q：你通常是使用紙和筆工作嗎？是否會使用計算機和LaTeX工作？

陶哲軒：實際上主要是紙和筆。在我的辦公室里，我有四塊巨大的黑板，有時候只需要把我所知道的關(guān)于問題的所有信息都寫在這上面，然后我會坐在沙發(fā)上，看著整個東西。

其中有很多繪畫和只有自己能理解的定制涂鴉。黑板的美妙之處在于可以擦除，但現(xiàn)在我也開始越來越多地使用計算機，部分原因是因為AI能執(zhí)行簡單的編碼工作，讓事情變得更加容易。

以前如果我想要繪制一個中等復(fù)雜度的函數(shù)，包含一些迭代或其它東西，我必須記住如何設(shè)置Python程序、以及循環(huán)如何工作并調(diào)試它，這需要兩個小時的時間。但現(xiàn)在我可以在10到15分鐘內(nèi)完成，所以我現(xiàn)在使用越來越多計算機進行簡單的探索。

總有算法來負責將一棵樹和另一棵樹進行匹配

Q：可以描述一下Lean形式化證明編程語言嗎？以及它是如何作為證明助手提供幫助的？

陶哲軒：Lean是一種計算機語言，就像Python和C等標準語言一樣，但在大多數(shù)語言中，重點在于產(chǎn)生可執(zhí)行代碼。代碼行會執(zhí)行一些操作，例如翻轉(zhuǎn)比特、讓機器人移動或在互聯(lián)網(wǎng)上發(fā)送文本等。

而Lean也是可以做到這一點的語言，可作為一個標準的傳統(tǒng)語言運行，但它也能生成證書。像Python這類軟件可能會進行計算并告訴你3+4的答案是7，但Lean不僅可以生成答案，還能生成它是如何得到7的證明，以及其中涉及的所有步驟。

它創(chuàng)建了更為復(fù)雜的對象，不僅僅是陳述，而是帶有證明的陳述。每一行代碼都只是將先前的陳述拼湊在一起，然后創(chuàng)建新陳述。

這個想法并不新鮮，它們被稱為證明助手。它們提供語言，讓你可以創(chuàng)建相當復(fù)雜精細的數(shù)學(xué)證明。如果你的編譯器可信，那它們會生成證書，確保你的觀點100%正確，但它們也會讓編譯器變得非常小，并且有多個不同的編譯器可用。

Q：你是否可以描述一下在紙筆上書寫和使用Lean編程語言之間的區(qū)別？形式化一個陳述有多難？

陶哲軒：很多數(shù)學(xué)家都參與了Lean的設(shè)計，所以它被設(shè)計成單獨的代碼行，類似于數(shù)學(xué)論證的單獨行。比如你可能想引入一個變量，證明一個矛盾。有很多你可以做的標準操作，理想情況下應(yīng)該是一一對應(yīng)的，但實踐中并非如此。

Lean就像向一個極其迂腐的同事解釋一個證明，他會指出，你真的是這個意思嗎？如果這個是零怎么辦？你如何證明這個？而Lean中包含很多自動化功能，可以減少麻煩。

例如，每個數(shù)學(xué)對象都必須包含一個類型，比如談?wù)揦，X是實數(shù)、自然數(shù)，還是函數(shù)或者其它，如果非正式數(shù)學(xué)，它通常需要有上下文，例如“顯然X是Y和Z之和，Y和Z是實數(shù)，那么X也應(yīng)該是實數(shù)。”

Lean可以做很多類似的事情，每隔一段時間它就會說，你能告訴我更多關(guān)于這個對象是什么的信息嗎？它是什么類型的對象？所以你必須在哲學(xué)層面上思考更多，不僅僅是你正在做的計算，而是每個對象在實際意義上代表什么。

Lex Fridman ：它是使用LLM進行類型推斷嗎？還是可以與實數(shù)匹配？

陶哲軒：它使用了更傳統(tǒng)的老式AI。你可以把這些東西都表示成樹，總有算法來負責將一棵樹和另一棵樹進行匹配。每個物體都有歷史可以追溯。

Lean是為可靠性而設(shè)計的，所以現(xiàn)代AI沒有被用在里面，它是一個完全不相關(guān)的技術(shù)。

所以當一個數(shù)學(xué)家試圖在Lean中編程一個證明時，通常會有這樣一個步驟，比如“好的，我現(xiàn)在想要使用微積分的基本定理來做下一步。”

所以Lean開發(fā)者構(gòu)建了這個龐大的項目mathlib，它是一個包含數(shù)萬個有關(guān)數(shù)學(xué)對象有用事實的集合，其中就有微積分基本定理，但你需要找到它，所以現(xiàn)在的很多瓶頸是引理搜索。

你可以有各種專門用于數(shù)學(xué)引理搜索的搜索引擎，但現(xiàn)在有了這些大型語言模型，你就可以直接詢問它們，例如當我編碼時，我在我的IDE中安裝了GitHub Copilot作為插件，它會掃描我的文本，看到我的需求。

當我需要使用微積分基本定理時，它會提供建議，25%的時間它完全正確，另外10-15%的時間它不完全有效，但足夠接近，然后我會告知它需要修改的地方，它就會生效，然后大約有一半的時間，它給我的是完全的垃圾。但人們開始在上面使用一點點人工智能，主要在自動補全的層面上，你可以輸入證明行的一半，讓它告知你另外一半。

所以我現(xiàn)在估計，將一個證明形式化出來所需的時間和精力大約是寫出來所花費的時間和精力的10倍，它是可行的，但很煩人。

這是它唯一迂腐的地方，但在某些情況下，形式化地做事情實際上更愉快。有一個我形式化了的定理，在最終陳述中存在常數(shù)12，12必須貫穿整個證明，所有其它數(shù)字都必須與這個最終數(shù)字12保持一致，所以我們寫了一篇圍繞著數(shù)字12的定理文章。

然后幾周后，有人說可以通過重新處理其中一些步驟，將12改進為11。當這種情況發(fā)生在紙筆上時，每改變一個參數(shù)，就必須逐行檢查證明的每一行是否仍然有效，并且可能存在一些你沒有意識到的微妙之處，你沒有意識到你在利用12的某些性質(zhì)，所以一個證明可能在微妙之處崩潰。

所以我們用常數(shù)12形式化了這個證明，當新論文出來時，花了我們20個人大約3周時間形式化。然后現(xiàn)在將12更新到11，在Lean里面直接修改就行， 然后運行編譯器，在所擁有的數(shù)千行代碼中，90%仍然有效，只有少數(shù)幾行標紅。

現(xiàn)在我無法證明這些步驟的正確性，但它立即隔離出哪些步驟你需要改變，你可以跳過所有正常工作的部分，只會有一小部分地方需要你修改。所以在一兩天內(nèi)，我們就把我們的證明更新到了11。這是一個非常快的過程，比紙筆要順利得多。

由于證明更長，每個單獨的部分更容易閱讀。例如當你拿到一篇數(shù)學(xué)論文，跳到第27頁，看第6段，這里有一行數(shù)學(xué)文本，我常常不能立即讀懂它，因為它假設(shè)了各種定義，我必須回去去找，也許10頁前定義了這個，證明總是分散在各處，所以你基本上被迫連續(xù)閱讀。

它不像小說那樣，可以打開一半開始讀，這里存在很多上下文。但當證明在Lean中時，如果你把光標放在某一行代碼上，那里的每個對象，你都可以讓光標懸停，它會說出這是什么，來自哪里，在哪里被證明。這比翻閱數(shù)學(xué)論文更容易回溯事物。

所以，Lean真正實現(xiàn)的一件事是，在原子尺度上協(xié)作證明，這在過去是無法做到的。所以傳統(tǒng)上，當你想與另一位數(shù)學(xué)家合作時，要么在黑板前進行真正的互動，要么通過電子郵件或其它方式，但必須進行分段，例如我要完成第3節(jié)，你做第4節(jié)，但不能真正在同一時間在同一件事上協(xié)作工作。

但有了Lean，你就可以嘗試形式化證明某一部分，然后說，我在第67行卡住了，我需要證明這個東西，但它并不完全有效，這是我有麻煩的三行代碼。由于所有上下文都在那里，別人可以說，好的，我知道你需要做什么，你需要應(yīng)用這個技巧或這個工具。

你可以進行極其原子級別的對話。因為Lean，我可以與世界各地的幾十個人合作，其中大多數(shù)人我從未見過面。實際上我也不知道他們在過程中是否可靠，但Lean給了我一份信任證書，這樣我就可以進行無信任數(shù)學(xué)。

Q：在合作時，解決數(shù)學(xué)難題的正確方法是什么呢？是分而治之，還是你會專注于某個特定部分，并且正在頭腦風暴？

陶哲軒：首先總是有一個頭腦風暴過程。對于數(shù)學(xué)研究項目，本質(zhì)上從一開始，你真的無從下手。它不像一個工程項目，理論已經(jīng)確立了幾十年，實施才是主要困難。你甚至必須弄清楚什么是正確的路徑。

就像我之前說的“作弊”，回到建橋的類比，首先假設(shè)你擁有無限的預(yù)算和無限的勞動力，現(xiàn)在你能建這座橋嗎？那現(xiàn)在有無限的預(yù)算但只有有限的勞動力，現(xiàn)在你能做到嗎？當然沒有工程師能真正做到這一點，因為他們有固定的要求。

在項目開始你總是會嘗試各種瘋狂的事情，做出所有不切實際的假設(shè)，但你計劃稍后再來修正解決。然后你會嘗試看看是否存在一個可能有效的方法框架，并寄希望于將問題分解為更小的子問題，然后你就可以專注于子問題。

有時不同的合作者更擅長處理某些事情。例如我和本·格林的一個定理，叫做格林-陶定理（the Green-Tao theorem）定理。它是一個關(guān)于素數(shù)包含任意長度的等差數(shù)列的陳述，這是對塞邁雷迪定理的一個修改。

而我們合作的方式是，本已經(jīng)證明了長度為3的等差數(shù)列含有一個類似的結(jié)果。他表明，像素數(shù)這樣的集合包含大量長度為三的數(shù)列，甚至素數(shù)的某些子集也包含。但他的技術(shù)只適用于長度為三的數(shù)列，不適用于更長的數(shù)列。

但我有這些來自遍歷理論的技術(shù)，這是我當時一直在玩的技術(shù)，我比本更熟悉。所以如果我能證明某些與素數(shù)相關(guān)的集合的特定隨機性性質(zhì)，就存在一定的技術(shù)條件擁有它。如果本能為我提供這個事實依據(jù)，我就可以得出定理。

但我要的是數(shù)論中一個非常困難的問題，他說我們不可能證明出來這個，所以他說，你能用一個弱假設(shè)來證明你的那部分定理嗎？他提出了一些他可以證明的東西，但對我來說太弱了，我不能用這個。所以類似的對話來回進行。

我們之間存在不同的作弊方式，我想作弊更多，他想作弊更少。但最終我們找到了一種屬性：A、他能證明；B、我可以使用，然后我們就可以證明我們的定理。所以要知道每次合作都會發(fā)生一些故事，沒有兩次完全相同。

Lean可以幫助科學(xué)家大規(guī)模地生產(chǎn)實驗結(jié)果

Q：如何看待Lean這一類編程語言？

陶哲軒：目前只有少數(shù)數(shù)學(xué)項目可以以這種方式劃分，在當前的技術(shù)水平下，大部分的Lean活動都是在形式化人類已經(jīng)證明的定理，基本上一個數(shù)學(xué)論文就是一個定理或一種意義上的藍圖。

Lean可以將一個困難的陳述，比如一個大的定理，分解成100個小的引理，但通常不是所有的定理都寫得足夠詳細以至于每一個都可以直接分解。

而藍圖就像一份非常繁瑣的論文，其中每一步都盡可能詳細地解釋，并試圖使每一步都相對獨立，僅依賴于少數(shù)幾個已證明的前置陳述，因此藍圖中的每個節(jié)點都可以獨立處理，甚至不需要了解整個系統(tǒng)的運作方式。

嗯，這就像現(xiàn)代供應(yīng)鏈，如果你想要制造一部 iPhone 或其他復(fù)雜物體，沒有人能夠獨立完成整個物體，但你可以讓一個專家，如果他們從其他公司獲得一些部件，就能將它們組合成稍大一些的部件。

Lex Fridman：我認為這是一個非常令人興奮的可能性，因為如果找到可以按這種方式分解的問題，就能擁有分布在全球各地的、成千上萬的貢獻者，是這樣么？

陶哲軒：對的。目前大多數(shù)數(shù)學(xué)都是理論性的，而實驗性數(shù)學(xué)則相對較少，我認為像Lean和其他軟件工具，比如GitHub之類的，將允許實驗數(shù)學(xué)以比我們現(xiàn)在所能做到的更大程度進行規(guī)模化。

現(xiàn)在如果你想要做任何關(guān)于數(shù)學(xué)模式或什么的數(shù)學(xué)探索，你只需要寫一些代碼來描述這個模式。我的意思是，有時候有一些計算機代數(shù)軟件包會提供幫助，但通常只是由一位數(shù)學(xué)家編寫大量的Python或其他代碼。畢竟編程是一項容易出錯的活，所以讓其他人協(xié)作編寫你的代碼模塊并不實際，因為如果其中一個模塊有bug，整個系統(tǒng)就不可靠。

這些定制的意大利面條式的代碼，由不是專業(yè)程序員而是由數(shù)學(xué)家編寫的，它們笨拙而且緩慢，所以很難大規(guī)模地生產(chǎn)實驗結(jié)果。但是有了Lean，數(shù)學(xué)家就能更好地進行這些工作。我有一個項目叫方程理論項目，在這個項目中我們生成了大約 2200 萬個抽象代數(shù)的小問題。

△圖片來源于方程理論項目頁

抽象代數(shù)研究乘法和加法等運算以及抽象的性質(zhì)，比如乘法的交換律，XY總是等于YX，至少對數(shù)學(xué)來說是這樣，這些運算遵循一些其它運算不遵循的法則。但并非所有的法則都是通用的，任何操作都可能遵循其它操作不遵循的法則，所以我們生成了大約4,000種可能的代數(shù)法則，以適應(yīng)不同的運算。

我們的問題是哪些法則會隱含哪些其他法則？嗯，例如，交換律是否隱含結(jié)合律？答案是否定，因為事實證明你可以描述一個操作，它遵守交換律但不遵守結(jié)合律，但另外一些法則確實蘊含其它法則，有時它們可以彼此替換，可以用一些代數(shù)進行證明。因此我們研究了這4000條法則之間的配對，大約有2200萬對組合，對于每一對我們都會問：這條法則是否蘊含了那條法則？如果是，請給出證明；如果不是，請給出反例。

這2200萬個問題，每一個問題都可以交給一個本科生代數(shù)學(xué)生，他們有相當大的機會能夠解決這些問題。盡管在這2200萬個問題中，有少數(shù)幾個，比如100個左右，確實非常難，但是很多問題都很簡單。這個項目的目標就是確定整個圖里哪些法則暗示了其它的法則。

Lex Fridman：這真是一個了不起的項目，一個好主意、好測試。這正是我們一直在討論的問題，規(guī)模令人矚目。

陶哲軒：是的，所以這種事情交給人工是不太可行的，我的意思是，最先進的技術(shù)在文獻中大約會有15 個方程以及它們的應(yīng)用方式，這差不多就是人類研究論文所能達到的極限了。如果你需要將規(guī)模擴大，就需要把這個項目眾包，還需要信任——沒有人能檢查 2200 萬個這些證明。你需要實現(xiàn)自動化，這只有在有了Lean之后才成為可能。

我們也希望大量使用人工智能，所以這個項目已經(jīng)接近完成了：在這2200萬個證明中，只剩下2個沒有得到解決。而實際上，關(guān)于這兩個，我們有兩份紙筆證明，今天早上我還在努力完成它。所以這個項目我們幾乎完成了。

Lex Fridman：這太厲害了，你能夠招募到多少人去完成這個項目？

陶哲軒：50個左右 ，這在數(shù)學(xué)上被認為是一個巨大的數(shù)字。所以我們有一篇有50位作者的論文，還有一個大的附錄說明每個人貢獻了什么。

Q：在這種多人參與的項目中，有沒有一種類似ELO評分的情況，可以根據(jù)貢獻者的專業(yè)水平來為他們的貢獻打分？

陶哲軒：這些精益項目的美妙之處在于，你可以自動獲取所有這些數(shù)據(jù)，你知道，所有內(nèi)容都必須上傳到 GitHub，而 GitHub 會追蹤誰貢獻了什么。所以你可以在任何時間點生成統(tǒng)計數(shù)據(jù)，你可以說，哦，這個人貢獻了這么多行代碼或者其他什么的。但這些都是非常粗糙的指標，我不希望這會成為人們晉升評審的一部分。

不過我想在企業(yè)計算領(lǐng)域，人們已經(jīng)在使用這些指標作為評估員工績效的一部分了，再次強調(diào)，這是一個有點可怕的方向，會導(dǎo)致學(xué)術(shù)水平下降，我們不喜歡指標。

Lex Fridman：但學(xué)術(shù)界卻在使用它們，只是使用的是舊指標，像論文數(shù)量。感覺這是一個有缺陷的指標，但也正朝著正確的方向發(fā)展，對嗎？

陶哲軒：是的，我認為研究它很有趣，我們可以做研究來判斷這些是否是更好的預(yù)測指標。有一個發(fā)現(xiàn)叫作古德哈特定律 (Goodhart’s law)，如果一個統(tǒng)計數(shù)據(jù)實際上被用來激勵表現(xiàn)，它就會變成一種游戲，而不再是一種有用的衡量標準。

因此，我們這個項目采用的是自我報告的形式。實際上，在科學(xué)領(lǐng)域存在關(guān)于人們貢獻類型的標準分類，有概念、驗證、資源提供、編程等等。有一個包含12個左右類別的標準列表，嗯，我們要求每位貢獻者在一個包含所有類別所有作者的巨大矩陣中，在他們認為自己做出貢獻的地方打勾，并且給出一個粗略的想法。比如你可能做了一些編程工作、提供了一些計算資源，但沒有做任何紙筆驗證或其他工作什么的……

傳統(tǒng)上數(shù)學(xué)家們只是按姓氏的字母順序排列，而我們沒有這種傳統(tǒng)，科學(xué)也有第一作者、第二作者的劃分等等，我們也沒有。我們?yōu)榇烁械津湴粒驗槲覀冏屗凶髡邠碛衅降鹊牡匚弧?/p>

但它也不能完全上升到這個高度。十年前我參加了一個一些被稱為“多數(shù)學(xué)者項目”的事情，它是眾包數(shù)學(xué)，那時候還沒有Lean，所以它受限于需要一個主持人來檢查所有提交的貢獻是否真正有效，這實際上是一個巨大的瓶頸。嗯，我們?nèi)匀挥幸恍╉椖坑?0位作者左右，但我們當時已經(jīng)決定不要試圖劃分每個人做了什么，而是共同使用一個假名，因此我們以 Bwaki 的精神為基礎(chǔ)，創(chuàng)造了一個名為DHJ Polymath的虛構(gòu)人物，Bwaki是20世紀一群著名數(shù)學(xué)家的筆名。

當時的論文是以DHJ Polymath這個筆名來發(fā)表的，所以我們都沒有獲得作者署名。實際上這不算一個好結(jié)果，原因有幾點，其中的一點是，如果你想要被考慮終身教職或者什么，你不能使用這篇論文作為你的出版物之一去提交，因為你沒有正式的作者署名。另一件事情是，直到很久以后人們才意識到，當人們提到這些項目時，只會提到項目中參與的最著名的人，而不是其他參與者。

所以這次我們嘗試了一些不同的：讓每個人都有作者身份，同時附上這個矩陣來解釋它如何運作。

Lex Fridman：僅僅是參與這樣的大型合作項目就足夠出色了。我看過幾年前Kevin Buzzard關(guān)于 Lean 編程語言的一個演講，你說這可能是數(shù)學(xué)的未來，這一點也很讓人興奮——世界最偉大的數(shù)學(xué)家之一也在擁抱這個似乎正在開創(chuàng)數(shù)學(xué)未來的東西。

DeepMind的AlphaProof系統(tǒng)

Q：DeepMind的AlphaProof系統(tǒng)是通過強化學(xué)習訓(xùn)練的，使用的數(shù)據(jù)包括國際數(shù)學(xué)奧林匹克(IMO)問題在Lean中成功和失敗的形式化證明，這屬于較高水平的高中數(shù)學(xué)問題。這個系統(tǒng)怎么樣？證明高中級別問題的系統(tǒng)與研究生級別問題之間存在著怎樣的差距？

陶哲軒：隨著證明中步驟數(shù)量的增加，難度會呈指數(shù)級增長，這是一次組合式爆炸。大型語言模型的問題在于它們會犯錯誤：如果一個證明有20個步驟，而你的模型在每個步驟中有10%的失敗率去走向錯誤的方向，真正到達終點的可能性很小。

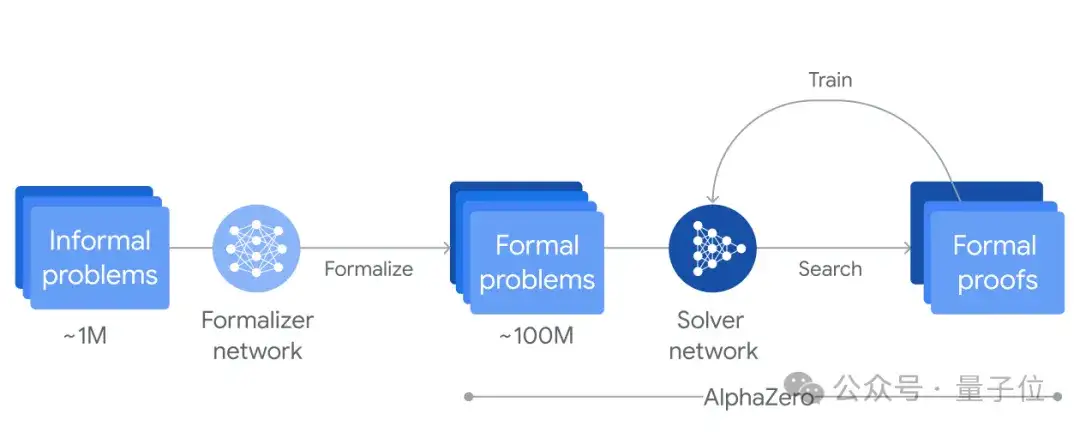
△圖片來源于AlphaProof項目頁

Lex Fridman：稍微扯一下題外話——從自然語言映射到形式程序的問題有多難？

陶哲軒：是的這實際上非常難，自然語言有很強的容錯能力，你可以犯一些小的語法錯誤，第二語言的說話者還是能大致理解你在說什么；但是形式語言，如果你有一個小地方出錯，整個事情就都成了無稽之談。甚至形式到形式都非常困難，不同語言中存在不同的、互不相容的序言，有Lean、Coq和Isabelle等等，即使從形式語言轉(zhuǎn)換到形式語言，依然是一個基本尚未解決的問題。

Lex Fridman：但是一旦你有了他們使用的非正式語言，他們就會用 RL 訓(xùn)練模型，用類似于AlphaZero的模型去嘗試提出證據(jù)。他們還有一個模型，我相信是用于幾何問題的獨立模型。那么這個系統(tǒng)給你留下什么樣的印象呢？你怎么看待這些差距？

陶哲軒：我們之前討論過，隨著時間的推移，一些令人驚嘆的事情會變得有些常態(tài)化。當然，幾何是一個可以解決的問題，這些都是很偉大的作品，展示了什么是可能的。但這個方法目前還不具備可擴展性，Google服務(wù)器時間要用三天時間去解決一道高中數(shù)學(xué)題。隨著復(fù)雜性的指數(shù)級增加，這并不是一個可拓展的前景。

Lex Fridman：我們需要提一下他們獲得了銀牌。

陶哲軒：只是相當于銀牌表現(xiàn)。首先，他們花費的時間遠超規(guī)定時限，而且是在人類協(xié)助下完成形式化驗證的。但既然解決方案獲得了滿分評定——我想這是因為通過了形式化驗證——所以這種評判應(yīng)該算是公平的。

事實上已經(jīng)有人提議要舉辦一場”AI數(shù)學(xué)奧林匹克競賽”。具體設(shè)想是：在人類選手參加正式奧林匹克競賽的同時，AI系統(tǒng)也將同步獲得相同的賽題，并在相同的時間限制內(nèi)作答，所有解答結(jié)果都將由同一批評委進行評分。這意味著AI必須使用自然語言而不是形式化語言來完成證明。

但我希望下一屆IMO比賽不會出現(xiàn)這種情況——這次IMO的表現(xiàn)確實在時間限制內(nèi)不夠理想。不過，在一些規(guī)模較小的競賽中，比如那些只需要給出具體數(shù)字答案而非完整證明過程的比賽，AI的表現(xiàn)其實要好得多。因為對于這類有明確數(shù)值答案的問題，強化學(xué)習會更容易一些：你得到了正確答案、你得到了錯誤答案，這是非常明確的信號。

但長篇證明要么必須正式，這樣Lean系統(tǒng)才能給出贊同或反對的反饋；要么就是非正式的，需要人類來評分。如果你試圖進行數(shù)十億次的強化學(xué)習運行，你知道，你無法雇傭足夠多的人來對這些進行評分。實際上，光是基于常規(guī)文本進行強化學(xué)習對當前的語言模型來說已經(jīng)很有挑戰(zhàn)性了，而現(xiàn)在如果不僅要雇傭人工審核員給出好評或差評，還要對輸出結(jié)果進行嚴格的數(shù)學(xué)驗證……這樣做的成本實在太高了。

“嗅覺”是人類特有的優(yōu)勢

Q：人類在數(shù)學(xué)領(lǐng)域最獨特的能力是什么？哪些方面是AI短期內(nèi)難以突破的？

陶哲軒：我認為數(shù)學(xué)家們所做的工作的性質(zhì)隨著時間的推移發(fā)生了很大的變化。

一千年前，數(shù)學(xué)家需要計算復(fù)活節(jié)的日期——那涉及極其復(fù)雜的運算，但這些計算早在一個世紀前就被自動化取代了。他們過去還要運用球面三角學(xué)進行航海導(dǎo)航，完成從舊大陸到新大陸的復(fù)雜計算，這些也都實現(xiàn)了自動化。

即使在AI出現(xiàn)之前，像Wolfram Alpha這樣的工具（雖然它不是語言模型）已經(jīng)能解決許多本科階段的數(shù)學(xué)問題。在計算層面，驗證常規(guī)問題——比如給出一個偏微分方程題目，要求AI用20種標準解法的其中一種求解——AI可以回答：”我已嘗試全部20種方法，這里有100種不同的排列，這是我的結(jié)果。”這類任務(wù)AI將表現(xiàn)得非常出色。一旦你解決了其中一個問題，就可以讓AI攻擊100個相似的變體。

但人類仍然保有獨特的優(yōu)勢：當前AI最大的短板在于，當它走錯路時它可能會說：”我要把問題拆分為兩種情況，嘗試這個技巧。”對于簡單問題，運氣好時這個方法有效；但有時它提出的解題思路完全是胡說八道，即使看上去像模像樣。這是語言模型生成數(shù)學(xué)內(nèi)容很讓人頭疼的地方。

確實，人類撰寫的低質(zhì)量數(shù)學(xué)內(nèi)容我們也見過不少，比如缺乏正規(guī)訓(xùn)練者的投稿。但糟糕的人類證明通常能快速識別，它會犯一些非常基本的錯誤；而AI生成的證明卻可能表面完美無瑕，因為強化學(xué)習實際上就是訓(xùn)練它們?nèi)ド煽雌饋硐袷钦_的文本，這對許多應(yīng)用場景來說這就已經(jīng)夠了。所以錯誤往往非常隱蔽，等你找到它們時，又會發(fā)現(xiàn)它們真的很愚蠢，因為沒有人會真的犯這種錯誤。

Lex Fridman：是的，這在編程環(huán)境下非常令人沮喪，因為我自己也經(jīng)常編程。當人類寫低質(zhì)量代碼時，有一種叫做代碼異味（code smell）的東西，你可以立刻看出來異常跡象。但AI生成的代碼從表面看起來完美規(guī)范，直到最后你才發(fā)現(xiàn)其中隱藏著極其明顯的愚蠢錯誤，偏偏這些錯誤還藏在看似良好的代碼結(jié)構(gòu)里。

陶哲軒：嗅覺是人類特有的一種東西，嗯，還有一種比喻性的數(shù)學(xué)嗅覺，但這個我們不清楚如何讓 AI 復(fù)制它。Alpha Zero等程序在圍棋和國際象棋等領(lǐng)域取得了一定的進展，在某種程度上，它們已經(jīng)發(fā)展出了一種對圍棋和國際象棋局勢的嗅覺，它們知道這個局勢對白方有利，對黑方有利。即使無法闡明原因，僅僅擁有這種“嗅覺”就讓它們能夠制定策略。

所以如果人工智能獲得某種評估特定證明策略可行性的能力，你可以說：“我打算把這個問題分解成兩個小子任務(wù)”，它們可以說：“嗯，這個看起來不錯，這兩個子任務(wù)看起來比你的主要任務(wù)更簡單，而且它們?nèi)匀挥泻芎玫臋C會實現(xiàn)，值得一試。”或者“哦不，你讓問題變得更糟糕了，因為這兩個子問題實際上比你原本的問題還要難。”這種情況實際上經(jīng)常發(fā)生，當你嘗試一些隨機的方法，很容易把問題變得更加復(fù)雜而不是變得簡單。所以，如果AI能夠擁有“嗅覺”，那它們也許可以開始和人類水平的數(shù)學(xué)家媲美。

Lex Fridman：這是一個難題，但不是競爭，而是合作。我們假設(shè)一下，如果我給你一個能夠做到你某些方面的能力的預(yù)言機，你可以與之合作，你希望那個預(yù)言機能做什么？你是否會希望它成為一種驗證器，去檢查代碼異味，就像你本人那樣？陶教授，這是一個充滿希望、富有成果的方向。或者你想讓它生成可能的證明，然后由你來看哪一個是正確的？你喜歡的話，或許還可以生成不同的表現(xiàn)形式，用完全不同的方式去看待同一個問題？

陶哲軒：是的，我認為以上選項都有可能，很多時候我們不知道如何使用這些工具，因為這是一種范式。過去我們從未遇到過如此矛盾的AI系統(tǒng)——它們既能理解復(fù)雜指令并處理海量任務(wù)，又會在細微處表現(xiàn)出令人不安的不穩(wěn)定性，同時卻仍能產(chǎn)出相當優(yōu)質(zhì)的結(jié)果。這種既強大又不可靠的特性組合確實耐人尋味。

這就像同時具備了兩種特質(zhì)的混合體：一方面如同可以深入交流的研究助手，另一方面又像傳統(tǒng)軟件工具那樣具備規(guī)模化運行能力，只不過前者無法規(guī)模化，后者又太過局限。Tim Gowers早在2000年就預(yù)見到了這種數(shù)學(xué)協(xié)作場景，說來有趣，距今正好二十多年。他在文章中設(shè)想了一個未來數(shù)學(xué)助手與人類數(shù)學(xué)家的對話場景：人類提出創(chuàng)意構(gòu)想，AI負責評估可行性；AI也會主動建議”需要驗證100個特例嗎”；或是實時反饋”你說命題對所有n成立，但我發(fā)現(xiàn)n=46時出現(xiàn)反例”。這種自由流動的協(xié)作模式正是我們所期待的：人類和AI雙方隨機提出想法或計算需求，沒有預(yù)設(shè)路徑。

我測試過這種協(xié)作方式，故意用已知答案的問題與AI合作。但當我建議使用某種方法時，AI往往會另辟蹊徑。有時它能發(fā)現(xiàn)精妙的論證思路，有時卻會完全偏離正軌，這時就不得不打斷：”不對不對，這個方向錯了，使用這個方法。”好的，它可能就會開始使用我提出的方法，然后回到我們期望看到的路徑。但你必須一直去引導(dǎo)它，才能讓它走上你想要的路徑，讓它更像你，最終才能強迫它給出你想要的證明。

就像是要趕一只貓一樣，嗯，我需要付出的個人努力，不僅在于引導(dǎo)它，還要去檢查它的輸出，因為它看上去能成功但實際上并不可以。這比自己做還要累得多，但這就是當前最先進的水平。

Lex Fridman：我想知道是否會發(fā)生一個階段性的轉(zhuǎn)變，以至于不再感覺像是在趕貓，也許它的發(fā)展速度會讓我們感到驚訝。

陶哲軒：我相信會。在形式化方面，我之前提到過，形式化一個證明比用手寫要花費 10 倍的時間。但用這些現(xiàn)代 AI 以及更好的工具，Lean的開發(fā)者們正在做得更加出色，他們不斷增加更多功能并使其更用戶友好，這個時間正在從9倍降到8倍再降到7倍……好的，這沒什么大不了，但終有一天它會低于1。這就是一個階段性的轉(zhuǎn)變。

因為當你寫論文的時候，它忽然就有意義了。先用Lean語言完成證明，或是通過與AI實時協(xié)作完成內(nèi)容，這個流程將變得理所當然，而期刊審稿流程也將隨之革新：對于已經(jīng)通過Lean形式化驗證的論文，審稿人只需要評估研究成果的重要性和它與現(xiàn)有文獻的關(guān)聯(lián)性，而不需要過度擔心證明過程的正確性，因為這些都是已被系統(tǒng)認證過的。

數(shù)學(xué)領(lǐng)域的論文正在變得越來越長，實際上，除非它們非常重要，否則為那些真正長的論文找到好的審稿人越來越難。這確實是一個問題，而形式化恰好在合適的時間出現(xiàn)，使得這種情況變得更容易猜測。

Lex Fridman：隨著工具鏈的完善和其他相關(guān)因素的發(fā)展，我們可以預(yù)見Mathlib這類數(shù)學(xué)知識庫很可能呈現(xiàn)指數(shù)級增長，這是一種良性循環(huán)。

陶哲軒：是的，我的意思是，LaTeX 如今已成為所有數(shù)學(xué)家使用的標準排版語言。過去人們使用各種文字處理器和打字機，但在某個時間點，LaTeX比其他所有的競爭對手都更容易使用，短短幾年內(nèi)就完成了整個學(xué)術(shù)界的徹底轉(zhuǎn)換，這種轉(zhuǎn)變堪稱戲劇性。

AI和菲爾茲獎的距離：差一個研究生

Q：距離 AI 系統(tǒng)作為合作者參與獲得菲爾茲獎級別證明的研究，我們還有多少年？換句話說，AI 何時能達到這種頂尖協(xié)作水平？

陶哲軒：這取決于AI和人類協(xié)作的水平。

Lex Fridman：我的意思是，它是否值得獲得菲爾茲獎。

陶哲軒：各占一半吧，如果這是一篇獲獎?wù)撐模渲邪恍?AI 系統(tǒng)協(xié)助寫作的話，你知道，就比如說，僅是完成順序就已經(jīng)…我使用它來加速我自己的寫作。比如說，你可以有一個定理，有一個證明，證明分為三個情況，我寫下第一個情況的證明，而自動補全建議：“現(xiàn)在，這里是第二個情況證明該如何進行”，并且它完全正確，太棒了，節(jié)省了我大約5到10分鐘的打字時間。

Lex Fridman：但在那種情況下，AI系統(tǒng)并不會獲得菲爾茲獎。我們是談?wù)?0年、50年還是100年？你覺得呢？好吧。

陶哲軒：我曾經(jīng)發(fā)表過一個預(yù)測，到2026年——也就是明年——將會出現(xiàn)AI和數(shù)學(xué)的合作，不是獲得菲爾茲獎的那種，而是實際研究水平的數(shù)學(xué)，比如一些由 AI 部分生成的、已發(fā)表的想法。也可能不是想法本身，但至少是一些計算或者驗證工作。

Lex Fridman：這種情況已經(jīng)發(fā)生了嗎？

陶哲軒：已經(jīng)發(fā)生過了，是的。有些問題是通過復(fù)雜的流程解決的，即與 AI 對話來提出想法，然后人類去嘗試，盡管它有可能不適用。

Lex Fridman：但它會提出一個不同的想法。

陶哲軒：確實有一些數(shù)學(xué)成果，只有在人類數(shù)學(xué)家和AI的共同參與下才得以完成，但他們的功勞很難理清。我的意思是，盡管這些AI工具并不能復(fù)制數(shù)學(xué)運算所需要的所有技能，但它們可以復(fù)制其中的相當一部分，大概30%到40%，它們可以填補某些方面的空白。

編程就是一個很好的例子：用Python編程對我來講是一件很麻煩的事，畢竟我不是一個專業(yè)的程序員，但是AI大大降低了做這件事情的摩擦成本，它為我填補了這個空白。現(xiàn)在AI在文獻綜述方面已經(jīng)做得相當不錯了，但仍然存在一個幻覺的問題，你知道，有些時候它會給出一些完全不存在的參考文獻。但我認為這是一個能夠解決的問題，通過用正確的方式進行訓(xùn)練等等，或者可以使用互聯(lián)網(wǎng)進行驗證，在幾年之內(nèi)應(yīng)該就可以到達這樣的水平：當你需要一個引理時，你可以問AI，之前是否有人證明過這個引理？AI就會進行一次高級的網(wǎng)絡(luò)搜索，然后告訴你，這里有6篇論文提到了類似的情況。

我的意思是你現(xiàn)在就可以問它，它會給你6篇論文，但其中可能只有一篇是真實且與問題相關(guān)的、一篇真實但與問題無關(guān)，剩下4篇完全是憑空捏造出來的。AI現(xiàn)在確實有非零的成功率，但存在太多的垃圾信息，信號與噪聲的比率太差了，以至于它只有在你已經(jīng)大致了解需要的關(guān)系時才最有幫助。嗯，你只需要被提示、被提醒一篇已經(jīng)潛藏在你記憶中的論文，而不是幫助你發(fā)現(xiàn)那些你甚至沒有意識到但卻是正確引用的新內(nèi)容。但是當它做到時，那個正確的選項會被埋沒在其他一系列的糟糕選項中。

Lex Fridman：AI能夠自動生成一個靠譜的相關(guān)工作部分是一件很美妙的事情，它可能會帶來另一個階段的變化，因為它能正確地歸功于人，并幫人類跳出“是的”這個思維定式。

陶哲軒：現(xiàn)在有一個很大的障礙需要克服：這就像自動駕駛汽車，你知道，它的安全邊際必須非常高才行。所以，是的，所有AI應(yīng)用都存在“最后一公里”問題，它們可以開發(fā)出20%到80%的時間里都有效的工具，但這仍然不夠，事實上，在某些方面甚至更加糟糕。

Lex Fridman：換個方式來問菲爾茲獎的問題，你認為在哪一天它會讓你真正地感到驚訝？當你讀到頭條新聞關(guān)于AI做了某件事的報道，一種真正的突破，讓人驚呼”這是菲爾茲獎級別”，就像當年AlphaZero在圍棋領(lǐng)域的突破那樣。

陶哲軒：大概是十年，我能看到它做出兩個人們認為無關(guān)的事情之間的猜想，并且實際上很有可能正確并且有意義。目前的模型面臨著很多困難，我的意思是，舉個例子，物理學(xué)家夢想讓AI發(fā)現(xiàn)新的物理學(xué)定律，你知道，他們的夢想就是你只管將所有的數(shù)據(jù)喂給AI，它就能夠給出我們以前從未見過的新的規(guī)律。但實際上，目前的尖端技術(shù)甚至難以從數(shù)據(jù)里發(fā)現(xiàn)舊的物理規(guī)律，即使它發(fā)現(xiàn)了，也存在很嚴重的污染，也就是說它之所以能夠做到，只是因為它已經(jīng)在某個訓(xùn)練數(shù)據(jù)中得到了這個舊規(guī)律，比如說玻意耳定律，或者任何你試圖重構(gòu)的規(guī)律。

部分原因在于，我們并沒有針對于此的正確類型的訓(xùn)練數(shù)據(jù)，對于物理定律來說，我們并沒有一百萬個不同的宇宙，每個宇宙包含一百萬條自然定律。

雖然我們已經(jīng)發(fā)表了很多人們能夠證明的東西，以及最終被驗證的猜想，或者產(chǎn)生的反例，但是我們沒有關(guān)于那些被提出但很快被意識到是錯誤猜想的數(shù)據(jù)，然后人們說，哦，我們應(yīng)該實際上改變我們的主張，以這種方式修改它，使其更具合理性。一個像這樣的試錯過程是人類數(shù)學(xué)發(fā)現(xiàn)中真正不可或缺的一部分，但我們不記錄它，因為它很尷尬。

呃，我們會犯錯，但我們只愿意發(fā)表我們的成功，所以人工智能沒有辦法訪問這些數(shù)據(jù)來訓(xùn)練。我有時候開玩笑說，AI得去讀個研究生，真的，你知道得去上研究生課程、做作業(yè)、去辦公室、犯錯，嗯，得到關(guān)于如何改正錯誤的建議并從中學(xué)習。

龐加萊猜想：想象一個被揉皺并扭曲的球

Q：Grigori Perelman在七年時間里幾乎不與外界接觸，獨自解決了龐加萊猜想，這是個什么問題？也許再談?wù)凣rigori Perelman的這段經(jīng)歷？

陶哲軒：好的，這是一個關(guān)于彎曲空間的問題，地球就是一個很好的例子。你可以想象一個二維曲面，它可能是一個帶洞的環(huán)面，也可能有很多洞，而且表面可能有多種先驗拓撲結(jié)構(gòu)，即使你假設(shè)它是有界的、光滑的等等。我們已經(jīng)弄清楚了如何對曲面進行分類，初步近似地看，一切都由一種被稱為虧格的屬性決定，即這個曲面上有多少個洞：球體的虧格為0，環(huán)面的虧格為1，以此類推。

區(qū)分這些二維曲面的一種方法是，球體具有一種被稱為單連通性的特性，意味著如果你在球體上取任何閉合環(huán)路，它都可以被收縮成一個點，同時保持在曲面上，而環(huán)面并不具備這種性質(zhì)。如果你在一個環(huán)面的外部取一根繞著環(huán)面的繩索，它無法通過環(huán)面的那個洞，也就沒有辦法閉合并收縮成一個點。球體是唯一具有這種可收縮性性質(zhì)的曲面，直到球面經(jīng)過連續(xù)變形。這就是我想稱之為與球面拓撲等價的物體。

龐加萊在更高的維度上提出了相同的問題，但這變得難以可視化，因為你可以在三維空間中想象一個曲面，但作為一個彎曲的自由空間，我們對四維空間沒有很好的直觀理解，無法將三維空間嵌入到四維空間中，我們需要五個、六個甚至更高維度的空間。但無論如何，從數(shù)學(xué)上講，你仍然可以提出這個問題：如果你有一個有界的三維空間，它還具有這個單連通的性質(zhì)，即每一個閉合曲線都可以收縮，你能把它變成一個三維球體的版本嗎？這就是龐加萊猜想。

奇怪的是，在四維、五維甚至更高維度上，這個問題反而更容易解決——它首先在更高的維度上得到了解決——可能是因為某種程度上，它有更多的空間來變形，更容易把事物變成一個球體。但三維情況下真的很難，人們嘗試了多種方法，比如說某種剖分方法，把曲面分割成小三角形或四面體，然后根據(jù)這些面面如何相互作用來進行推導(dǎo)；或者也有代數(shù)方法，使用各種代數(shù)對象，比如所謂的“基本群”，你可以將它們附加到同調(diào)、上同調(diào)、以及所有這些非常高級的工具上。它們也沒能完全奏效。

但是Richard Hamilton提出了一個微偏分方程（PDE）的方法，問題是這樣的，你有一個球體，但它的呈現(xiàn)方式非常的奇怪：想象一個被揉皺并扭曲的球，讓人看不出來那是個球。如果你有一個某種意義上是變形球體的曲面，你可以將它想象成一個氣球，試著給它充氣，隨著空氣的注入，它的皺紋會被撫平，就變成了一個漂亮的球體；但如果它是個環(huán)面或者類似的東西，它就會在某個點卡住。當內(nèi)環(huán)收縮到零時，中間會得到一個奇點，并且無法再繼續(xù)膨脹或者流動了。Richard Hamilton創(chuàng)造了這個流程，現(xiàn)在被稱為里奇流（Ricci flow），這是一種把任意曲面或空間平滑化、變得越來越圓的方法，讓它看起來像個球體。這個過程要么會形成一個球體，要么就產(chǎn)生一個奇點。就像是偏微分方程，它們要么具有全局規(guī)劃性，要么就具有有限時間爆炸性，基本上這幾乎是完全相同的事情。一切都是相互關(guān)聯(lián)的。

Richard Hamilton指出，對于二維曲面，如果能保持永不形成奇點，就永遠不會遇到麻煩，它會一直流動，并且形成一個球體，于是他得到了二維結(jié)果的一個新的證明。

Lex Fridman：這是一個很棒的解釋，對于里奇流及其在此背景下的應(yīng)用。對于2D情況來說，這里的數(shù)學(xué)有多難？

陶哲軒：這些是非常復(fù)雜的方程，與愛因斯坦方程不相上下，額，略微簡單一些，但它們被認為是難以求解的非線性方程。2D中有很多特殊技巧可以提供幫助，但問題在于，在3D中這個方程實際上是超臨界（supercritical ）的。與納維-斯托克斯方程相同的問題，隨著爆發(fā)性增長，曲率可能會集中在越來越小的區(qū)域，并且看起來越來越非線性，情況變得越來越糟。

△納維-斯托克斯方程的一般形式

可能會出現(xiàn)各種各樣的奇點，其中一些可能存在于那些被稱為“脖子夾”（neck pinchers）的、表面像杠鈴一樣的地方，并且在某一點收縮；有些奇點足夠簡單，你可以從中間剪開，然后就能把一個表面變成兩個，并分別演化它們；但也存在這樣的可能性：會出現(xiàn)一種非常棘手的像打了結(jié)一樣的奇點，沒辦法對它進行任何“手術(shù)”。所以就需要對所有的奇點進行分類，比如知道事情可能會出錯的所有方法是什么。

Perelman首先做的是把問題從超臨界問題過渡到臨界問題，像我之前說過能源的發(fā)明，哈密頓量闡明了牛頓力學(xué)。他介紹了一些概念，現(xiàn)在稱為佩雷爾曼減少體積（Perelman’s reduced volume）以及佩雷爾曼的熵（Perelman’s entropy），并引入了新的量，比如能量，這些量在每個尺度上都保持一致。非線性實際上突然看起來不再像以前那么可怕了。

△Grisha Perelman證明龐加萊猜想的論文

他仍然需要分析奇點這一關(guān)鍵問題——這本身也是一個類似的問題——就難度上，和我所研究的波映射問題相當。所以Perelman設(shè)法對所有奇點進行了分類，并展示如何對每種情況進行處理。通過這種方式，他解決了龐加萊猜想。這包含了很多雄心勃勃的舉措，今天的大語言模型都沒辦法做到。我的意思是，我充其量只能想象一個模型會將這個想法在數(shù)百種嘗試方案中提出，但除此之外的99個將會是徹底的死路一條，而你只有在經(jīng)過幾個月的工作之后才能發(fā)現(xiàn)。Perelman肯定感覺到這是正確的道路才會去追求，因為從A到B要花費好幾年的時間。

Lex Fridman：嚴格從數(shù)學(xué)角度來說，或者更廣泛地，從流程上來說，你也做過類似困難的事情。你能從Perelman經(jīng)歷的過程中推斷出什么？因為他是獨自一人去完成這件事的。在這樣的過程中會遇到哪些低谷？就像人工智能不知道自己什么時候會失敗一樣，當你坐在辦公室里，意識到過去的幾天甚至幾周所做的事情是個失敗的時候，你會作何反應(yīng)？

陶哲軒：嗯，對我來說，我會換個問題。就像我說的，我是一只狐貍而不是一只刺猬。

Lex Fridman：但這是合理的，你可以休息一下，離開，去研究不同的問題。

陶哲軒：是的，你也可以修改這個問題，我的意思是，你可以去“作弊”，如果有什么東西阻礙了你，一些不好的情況不斷出現(xiàn)，你的工具不起作用什么的……你可以假設(shè)按理來講這種糟糕的情況不會發(fā)生，進行一些神奇的思考，從戰(zhàn)略上來講看看其它的論點是否成立。如果你的方法存在多個問題，那么你有可能就會放棄，但如果這是唯一的問題，其他的一切都順利的話——那么它仍然值得挑戰(zhàn)，你可以進行一些前方偵查什么的。

有時候犯錯誤甚至是有益的，我有一個項目確實因此贏得了一些獎項。和其他四個人一起，我們再次研究了這個PDE問題，實際上這又是一個爆破正則的問題，這種問題被認為非常困難。另一位菲爾茲獎得主Jean Bourgain曾經(jīng)研究過這種問題的特殊情況，但他沒能解決一般情況，而我們研究這個問題兩個月，以為我們解決了它。我們作出了一個可愛的論證認為一切都吻合，為此我們很興奮，我們計劃舉行慶祝活動，讓大家聚在一起喝點香檳什么的。我們開始寫它，然后我們中的其中一個人——不是我——另一位合著者說：“哦！在這個引理中，我們必須估算這個展開式中出現(xiàn)的13項，我們估算了其中的12項，但我們的筆記里卻找不到第13項，有人能找到它嗎？”然后我說：“好的，我會看看這個。”結(jié)果，好吧，我們完全忽略了這一項，并且這一項變得更糟糕了，比其他12項加起來還要糟糕。

事實上，我們沒辦法估算這個第13項，我們又嘗試了幾個月，嘗試了幾乎所有不同的排列組合，總有一個東西讓我們無法控制。這非常讓人沮喪。但因為我們已經(jīng)投入了好幾個月，并為此付出了好幾個月的努力，我們依然在堅持。我們嘗試了越來越絕望的、瘋狂的事情，兩年以后，我們找到了另外的一種方法，和我們最初的設(shè)想有些不同，這種方法并沒有產(chǎn)生這些有問題的項，而是確實解決了這個問題。所以我們用了兩年的時間解決了這個問題。但如果我們沒有那個看似即將解決問題的虛假希望，我們可能在第二個月左右就放棄，并著手去解決一個更簡單的問題了。如果我們知道要用2年的時間，我也不確定我們還會不會啟動這個項目。

有時候這些不正確的——就像哥倫布在新大陸航行一樣——這是一個測量地球大小的錯誤版本，他以為他會找到一條通往印度的新的貿(mào)易曲線，至少他在招股說明書上是這樣宣傳的，我的意思是，它實際上可能對此心知肚明。

Q：僅從心理因素來看，你有沒有產(chǎn)生過最讓你感到無措的自我懷疑？

Lex Fridman：感覺數(shù)學(xué)實在是太令人著迷了，當你在某個問題上投入太多精力但結(jié)果卻是錯誤的時候，它可能會擊潰你。就像是，國際象棋也擊潰了一些人。

陶哲軒：我認為不同的數(shù)學(xué)家對數(shù)學(xué)有著不同的情感投入程度，有些人認為這只是個工作，你遇到了問題，你可以不解決，而是繼續(xù)下一個，所以你總是可以繼續(xù)投入另一個問題，這減少了情感上的聯(lián)系。還有一些情況會產(chǎn)生一些被稱為數(shù)學(xué)病的問題，就是他們會只抓住那個問題不放，花費數(shù)年只思考那個問題，即使他們的職業(yè)生涯會因此受損。但他們說：“好吧，但這是個大突破，一旦我解決了這個問題，它將彌補所有失去機會的歲月。”這種心態(tài)偶爾確實有效，但我講真不推薦給沒有毅力的人。

我從來沒有對任何一個問題投入過多精力，一個幫助我們的點是，我們不需要提前明確我們的問題。當我們提交研究提案時，我們會說我們將研究這一系列問題，但即使我們不確定五年內(nèi)我肯定會提供所有這些問題的證明，而是承諾取得一些進展或發(fā)現(xiàn)一些有趣的現(xiàn)象。也許你沒能解決那個問題，但你發(fā)現(xiàn)了一個相關(guān)的、你可以對其說些新東西的問題，而那是一個更可行的任務(wù)。

加法和乘法都簡單，但是合在一起……

Q：有沒有一個一直困擾著你們的問題？像孿生素數(shù)猜想、黎曼猜想、克拉茲猜想？

陶哲軒：孿生素數(shù)，聽起來……好吧，再說，我的意思是，像黎曼猜想一樣，那真是遙不可及，甚至完全沒有可行的途徑。即使我使用了所有我知道的作弊手段，在這個問題里也依然無法從A到B。我認為首先需要在數(shù)學(xué)的其他領(lǐng)域取得突破，然后有人要認識到那個突破是可以運用于這個問題的。

Lex Fridman：所以我們應(yīng)該后退一步，只討論素數(shù)。它們通常被稱為數(shù)學(xué)的原子。你能談?wù)勥@些原子提供的結(jié)構(gòu)嗎？

陶哲軒：自然數(shù)有兩種基本運算：加法和乘法。所以如果你想生成自然數(shù)，你可以做兩件事之一：你可以從1開始，一次次地加1，這樣就生成了自然數(shù)，所以從加法角度看，它們很容易生成1、2、3、4、5；或者你可以取質(zhì)數(shù)，如果你想從乘法角度生成，你可以取所有質(zhì)數(shù)，2、3、5、7，然后把它們?nèi)砍嗽谝黄稹＿@樣你就得到可能除了1以外所有自然數(shù)。所以從加法和乘法角度看，自然數(shù)有兩種不同的思考方式。單獨來看，它們都不算太難，關(guān)于自然數(shù)的任何問題，如果是只涉及加法或乘法的，都相對容易解決。

令人沮喪的是，當你把這兩者結(jié)合起來，問題忽然就變得極其豐富……我的意思是，我們知道數(shù)論中有一些命題實際上是不可判定的。像是某些多元多項式方程是否存在自然數(shù)解的問題，它們的答案取決于數(shù)學(xué)基礎(chǔ)命題的不可判定性——比如數(shù)學(xué)公理本身的一致性。

但即使是最簡單的問題，把一些乘法和加法運算結(jié)合起來，比如在素數(shù)上做一些附加操作，像是移動2位。分別來說我們都很了解，但如果你問當你平移一個素數(shù)兩位時，能否得到一個另素數(shù)？或者你能多久得到另一個素數(shù)？將兩者聯(lián)系起來竟然變得如此困難。

Lex Fridman：孿生素數(shù)猜想就是這樣的，它假設(shè)存在無限多對相差為2的素數(shù)。有趣的是，你在回答這些種類繁多的復(fù)雜問題時取得了非常成功的進展，比如你提到的格林-陶定理，它證明了素數(shù)序列包含任意長的等差數(shù)列。你能證明出這樣的定理，真是令人難以置信。

陶哲軒：是的。所以我們意識到，這種類型研究的重點是不同的模式具有不同級別的不可摧毀性。孿生素數(shù)問題的難點在于，如果你把世界上所有的素數(shù)都列出來，3、5、7、11 等等，其中有一些是成對的，比如 11 和 13 是一對孿生素數(shù)，還有其他孿生素數(shù)等等。如果你愿意的話，你可以輕松地編輯素數(shù)以擺脫這些孿生素數(shù)。雖然孿生素數(shù)是無窮多的，但它們在素數(shù)里實際上相當稀疏，一開始確實有不少，但一旦到了數(shù)百萬、數(shù)萬億級別，它們就變得越來越稀少。實際上，如果有人能夠訪問素數(shù)數(shù)據(jù)庫，他們只需在這里或那里刪除幾個素數(shù)，就可以讓孿生素數(shù)猜想成為錯誤。只需要刪除0.01%的素數(shù)或者類似的什么，真是明智之舉。

因此，你可以提供一個經(jīng)過審查的素數(shù)數(shù)據(jù)庫，它通過所有關(guān)于素數(shù)的統(tǒng)計測試、遵循多項式定理和其他質(zhì)數(shù)效應(yīng)，但不再包含任何孿生素數(shù)。這對于孿生素數(shù)猜想來說是一個真正的障礙，意味著任何旨在在實際素數(shù)中找到孿生素數(shù)的證明策略，在應(yīng)用于這些稍作修改的素數(shù)時都必須失敗。因此，這必定是素數(shù)中某種非常微妙、精細的特征，而不僅僅是通過整體統(tǒng)計分析就能得到的。

另一方面，算術(shù)級數(shù)被證明要穩(wěn)健得多。你可以取素數(shù)，實際上可以排除 99%的素數(shù)，你可以選擇任意90個參與者。結(jié)果發(fā)現(xiàn)，我們另一個證明是，你仍然可以得到算術(shù)級數(shù)。算術(shù)級數(shù)非常多，它們就像蟑螂一樣。

Lex Fridman：對于不了解的人來說，算術(shù)級數(shù)是一系列相差某個固定值的數(shù)。

陶哲軒：是的。但它又像是那種無限猴子現(xiàn)象（一只猴子在無限時間內(nèi)隨機獨立地敲擊打字機鍵盤上的按鍵，幾乎肯定會打出任何給定的文本），對于任何固定長度的集合，你不會得到任意長度的進展，只會得到相當短的進展。

Lex Fridman：但你說孿生素數(shù)不是無限猴子現(xiàn)象。我的意思是，這是一只非常狡猾的猴子，但它仍然是一種無限猴子現(xiàn)象。

陶哲軒：如果素數(shù)真的是隨機的，這些素數(shù)是由猴子生成的，那么事實上無限猴子定理就是這樣的。

Lex Fridman：但你說是孿生素數(shù)，你不能使用同樣的工具。它看起來幾乎不是隨機的。

陶哲軒：嗯，我們不知道。我們相信素數(shù)的表現(xiàn)像是一個隨機集合。所以我們關(guān)心孿生素數(shù)猜想的原因，是一個測試案例，測試我們是否能夠真正地、自信地、假設(shè)錯誤率為0%，說素數(shù)表現(xiàn)得像是一個隨機集合。我們已知的素數(shù)的隨機版本至少有100%的概率包含孿生素數(shù)，或者隨著你越來越向外延伸，概率趨于 100%。所以，我們相信素數(shù)是隨機的。算術(shù)級數(shù)之所以不可摧毀，是因為無論它看起來是隨機的還是周期性的結(jié)構(gòu)，在這兩種情況下，算術(shù)級數(shù)都會出現(xiàn)，但原因不同。這就是這個定理的基本原理，有很多證據(jù)都證明了算術(shù)級數(shù)定理，它們都通過某種二分法得到證明：即你的集合要么是結(jié)構(gòu)化的，要么是隨機的，在兩種情況下你都可以說些什么，然后你把兩者結(jié)合起來。

但在孿生素數(shù)中，如果素數(shù)是隨機的，那么你很高興，你就贏了。如果素數(shù)是結(jié)構(gòu)化的，它們能夠以一種特定的方式結(jié)構(gòu)化并消除孿生素數(shù)。我們不能排除這個陰謀。

Lex Fridman：但據(jù)我了解，你可以做到在K元組（K-tuple）版本上取得進展。

陶哲軒：是的。所以關(guān)于陰謀的一個有趣之處是，任何一個陰謀理論都很難被證偽。如果你相信世界是由蜥蜴統(tǒng)治的，你會說“那么這里有一些證據(jù)表明它不是由蜥蜴統(tǒng)治的。”嗯，但是那個證據(jù)也是蜥蜴的陰謀，你可能遇到過這種情況。幾乎沒有辦法可以明確排除陰謀，在數(shù)學(xué)上也是如此，一個完全致力于消除孿生素數(shù)的陰謀還必須滲透到數(shù)學(xué)的其他領(lǐng)域，但至少據(jù)我們所知，它可以保持一致。但有一個奇怪的現(xiàn)象，你可以用一個陰謀排除其他陰謀。所以如果世界是由蜥蜴統(tǒng)治的，它就不能同時是由外星人統(tǒng)治的，對吧？

所以一個不合理的事情很難被證偽，但多個不合理的事情就有工具了。比如我們知道存在無限多個素數(shù)，其中任意兩個素數(shù)的差值不超過……實際上，這個數(shù)字最高是246，存在一個界限。所以有孿生素數(shù)；有一種東西叫做表親素數(shù)（cousin primes），它們的差值為4；還有相差6的性感素數(shù)（sexy primes）——這個概念遠沒有其名稱所暗示的那么令人興奮。

你可以排除其中一個陰謀，可一旦你有 50 個陰謀，事實證明，你無法一次性排除所有的可能性。這需要這個陰謀空間里太多的能量。

Q：你是怎么做界限部分的？你是怎么為不同的素數(shù)發(fā)展界限的？

陶哲軒：所以這最終是基于一個被稱為鴿巢原理（the pigeonhole principle）的東西。鴿巢原理就是，如果你有若干只鴿子，并且它們都必須進入鴿巢，而鴿子數(shù)量多于鴿巢數(shù)量，那么至少有一個鴿巢里必須有至少兩只鴿子。所以必定有兩只鴿子彼此距離很近。比如，如果你有 100 個數(shù)字，它們都介于 1 到 1000 之間，那么其中兩個數(shù)字之間的距離最多為 10，因為你可以將 1 到 100 的數(shù)字分成 100 個鴿巢。假設(shè)你有 101 個數(shù)字，那么這 101 個數(shù)字中必定有兩個數(shù)字之間的距離小于 10，因為這兩個數(shù)字必須屬于同一個鴿巢。這是數(shù)學(xué)基本原理的基本特征。

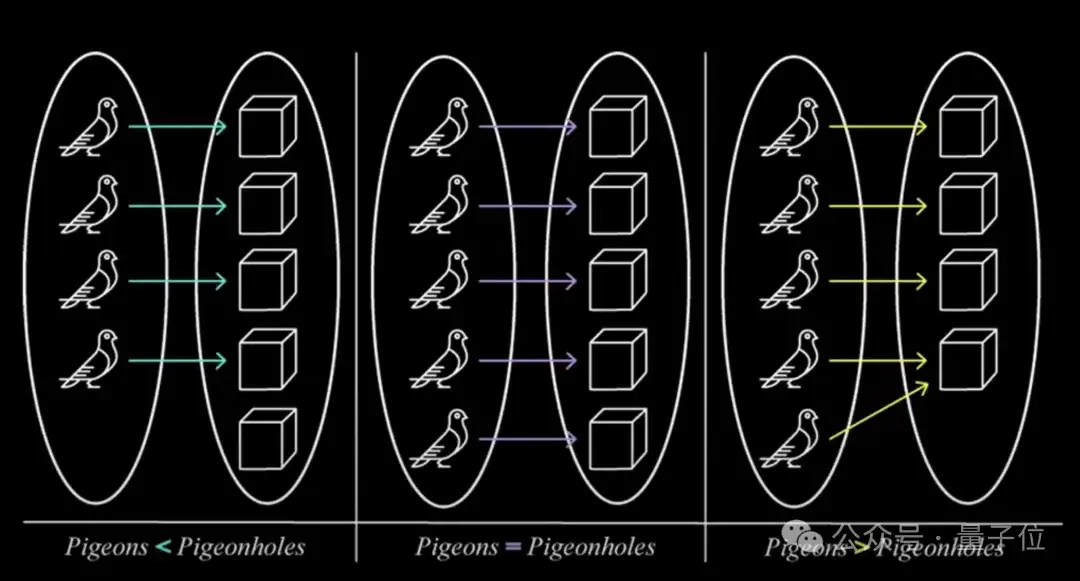
鴿巢原理不能直接和素數(shù)一起使用，因為素數(shù)在向外延伸時會變得越來越稀疏，也就是說質(zhì)數(shù)會變得越來越少。但事實證明，有一種方法可以給數(shù)字分配權(quán)重。有些數(shù)字算是準素數(shù)（almost primes ），但它們并非沒有除了自身和1以外的任何其他因數(shù)，只不過它們擁有的因數(shù)非常少。事實證明，我們對準素數(shù)比素數(shù)理解得更透徹。例如人們很早就知道存在孿生素數(shù)，這個問題已經(jīng)被研究透了。所以準素數(shù)是我們能夠理解的東西。因此，你實際上可以將注意力集中在合適的準素數(shù)集合上。素數(shù)相對來講非常稀疏，相比之下，準素數(shù)的稀疏程度要低得多。

你可以構(gòu)建一個準素數(shù)的集合，其中素數(shù)的密度大約是 1%，這能讓你有機會通過應(yīng)用某種鴿巢原理來證明大約只有100個素數(shù)。但為了證明孿生素數(shù)猜想，你需要獲得素數(shù)的密度，在準素數(shù)內(nèi)幾乎達到50%的閾值，一旦達到 50%，你就會得到孿生素數(shù)。但不幸的是，無論你選擇多么好的準素數(shù)集合，素數(shù)的密度永遠不會超過 50%，這就是所謂的“奇偶性壁壘”（the parity barrier）。我非常想攻克它，所以，我長遠的夢想之一是就找到一種方法來突破這個障礙，因為這將不僅解開孿生素數(shù)猜想，還能解開克拉茲猜想，和許多數(shù)論領(lǐng)域正在受阻的其它問題。因為我們的現(xiàn)有技術(shù)需要超越這個理論上的“奇偶性壁壘”，就像試圖超光速行駛一樣。

Lex Fridman：所以我們應(yīng)該說孿生素數(shù)猜想是數(shù)學(xué)史上最大的問題之一，克拉茲猜想也是，它們感覺像是鄰居。有沒有哪天你覺得自己看到了解法？

陶哲軒：有的。有時你嘗試某種方法，它就會非常有效，你就會感受到像我們之前談到的數(shù)學(xué)氣味（mathematical smell）。當事情進展順利時，你會從經(jīng)驗中學(xué)習，因為有一些困難是不得不去遭遇的。我的一位同事可能會這樣表達：如果你在紐約街頭被蒙上眼睛放進車里，在幾個小時后，你的眼罩被摘掉，發(fā)現(xiàn)你到了北京。我的意思是，這有點太容易了，不知道為什么并沒有跨越海洋，即使你不知道具體發(fā)生了什么，你會懷疑有些事情不對勁。

Lex Fridman：但這仍然在你腦海中，你是否每次都會回到素數(shù)領(lǐng)域看一會兒？

陶哲軒：是的，在我沒什么其他事情可做的時候——這種情況越來越少了，我現(xiàn)在有很多事情要處理——但當我有空閑時間，又不想做我的實際研究項目，也不想處理行政事務(wù)，或者不想為家人做些差事，我可以玩這些有趣的東西。通常情況下什么也得不到，你必須學(xué)會說：“好吧，再試一次，什么都沒發(fā)生，我會繼續(xù)前進。”偶爾我也會解決這些問題，或者有時就像你說的，你以為你解決了問題，然后你繼續(xù)研究可能 15 分鐘，然后你想到，“我應(yīng)該檢查一下，這簡單得有點令人難以置信了。”通常都是這樣。

Lex Fridman：關(guān)于孿生素數(shù)和克拉茲猜想這些問題的解決時間，你的直覺是怎么看的？

陶哲軒：關(guān)于孿生素數(shù)，我認為我們將會不斷獲得更多進展。這確實至少需要10年，這個“奇偶性壁壘”是剩下的最大的難題，有更簡單的版本，我們已經(jīng)非常接近這個猜想了。所以我認為在 10 年內(nèi)我們將會有更多更接近的結(jié)果，但可能不會得到全部。孿生素數(shù)問題相對接近，但黎曼猜想，我一點頭緒也沒有，我的意思是，我想這是偶然發(fā)生的。

Lex Fridman：所以黎曼猜想是關(guān)于素數(shù)分布的更普遍的猜想，是吧？

陶哲軒：是的。這表明，在某種程度上只從乘性角度來看，對于只涉及乘法不涉及加法的問題，質(zhì)數(shù)確實表現(xiàn)得像你希望的那樣隨機。

概率中存在一個現(xiàn)象稱為平方根抵消（square root cancellation），如果你想要調(diào)查美國民眾對某個問題的看法，并且只詢問一兩個選民，你可能會抽到一個糟糕的樣本，然后你會得到一個對整體平均值的非常不精確的測量。但如果你抽樣的人數(shù)越來越多，準確性就會越來越好，并且準確性隨著你抽樣人數(shù)的平方根而提高。如果你抽樣 1,000 人，你可以得到 2%或 3%的誤差范圍。在同樣的意義上，如果你以某種乘法性方式測量質(zhì)數(shù)，你可以測量某種類型的統(tǒng)計數(shù)據(jù)，它被稱為黎曼zeta函數(shù)，并且上下波動。

但從某種意義上說，隨著你不斷取更多平均值、不斷進行更多采樣，波動應(yīng)該會像隨機變量一樣減小。并且有一種非常精確的方法來量化這一點。

黎曼猜想以一種非常優(yōu)雅的方式捕捉了這一點，但就像數(shù)學(xué)中的許多其他方法一樣，我們幾乎沒有工具來證明某件事真的表現(xiàn)得非常隨機。這實際上不僅僅是一點點隨機，但這種平方根抵消要求其行為像一個真正隨機的集合一樣隨機。我們知道，對于與奇偶性校驗問題有關(guān)的事情，大多數(shù)的常用技術(shù)都無法解決。證明必須出乎意料，但沒有人提出過任何嚴肅的提議。正如我所說，有很多種方法可以解決，你可以稍微修改一下質(zhì)數(shù)，就可以破壞黎曼猜想。它必須非常精細、你不能應(yīng)用具有巨大誤差范圍的東西、它必須能夠勉強工作，所有的這些陷阱你都會遇到并且非常嫻熟地躲避。

Q：對你來說，素數(shù)最神秘的是什么？

陶哲軒：這是個好問題，從推測上來說，我們對素數(shù)有一個很好的模型。我的意思是它們具有某些規(guī)律，比如質(zhì)數(shù)通常是奇數(shù)。但除了存在一些明顯的規(guī)律外，它們表現(xiàn)得非常隨機，只是假設(shè)它們會這樣表現(xiàn)。

所以有一個稱為 Cramér質(zhì)數(shù)隨機模型的東西，在某個時間點之后，素數(shù)的表現(xiàn)就像一個隨機集合。這個模型還有各種細微的修改，但這是一個非常好的模型，它與數(shù)值相匹配，并告訴我們應(yīng)該預(yù)測什么。就像是我告訴你可以完全肯定孿生素數(shù)猜想是正確的。隨機模型給出了極高的準確性，我只是無法證明這一點。我們的數(shù)學(xué)大多是為了解決包含規(guī)律的問題而優(yōu)化的。而質(zhì)數(shù)存在這種反模式，實際上幾乎所有事物都是這樣，但我們無法證明這一點。

我想質(zhì)數(shù)是隨機的并不神秘，因為它們沒有必要有任何秘密模式。但神秘的是，究竟是什么機制真正迫使隨機性發(fā)生？這一點完全缺失。

克拉茲猜想：賭桌上沒有贏家

Q： 克拉茲猜想陳述簡單而富有美感，解決起來卻極其困難。Paul Erdos關(guān)于克拉茲猜想說過，數(shù)學(xué)可能還沒有準備好解決這類問題。還有人表示這是一個極其困難的問題，完全超出了當前數(shù)學(xué)的范疇——這是在 2010 年的說法，但你已經(jīng)取得了一些進展。為什么如此難以解決？你能解釋一下它到底是什么嗎？

陶哲軒：這是一個可以解釋的問題，借助一些視覺輔助工具會更有幫助。你可以取任何一個自然數(shù)，比如 13，然后對它應(yīng)用以下步驟：如果它是偶數(shù)，就除以2，如果是奇數(shù)，就乘以3再加1。這樣做，偶數(shù)會變小，奇數(shù)會變大，所以13會變成40，因為13乘以3是39，加1就得到40。這是一個簡單的過程。對于奇數(shù)和偶數(shù)，它們都是非常容易的操作。然后把它們結(jié)合起來，仍然相當簡單。

但接著你會問，迭代它會發(fā)生什么？把剛剛得到的輸出反饋回去，所以13變成40，40現(xiàn)在是偶數(shù)，除以2是20；20仍然是偶數(shù)，除以2是10，5；然后5乘以3加1是16；然后是8，4，2，1；然后從1開始，它會變成1，4，2，1，1，4，2，1，無限循環(huán)。

所以，我剛才描述的這個序列，13，40，20，10，這些都是所謂的冰雹序列，有一個關(guān)于冰雹形成的過于簡化的模型，這個模型實際上并不完全正確，但仍然以初步近似的身份被教給高中生。這個模型是：一個小冰塊形成冰晶并懸浮在云中，因為風的作用上下移動，有時在寒冷時它會獲得一些質(zhì)量，也許也會稍微融化一點。這個上下移動的過程形成了部分融化的冰，最終導(dǎo)致冰雹的形成，然后它最終會落到地球上。

克拉茲猜想是，無論你從多高的地方開始，你取一個數(shù)，這個數(shù)可能是數(shù)百萬或數(shù)十億，這個上下移動的過程，如果你是奇數(shù)就上升，是偶數(shù)就下降，它最終總會落到地球上。

Lex Fridman：也就是說無論你從這個非常簡單的算法的哪里開始，你最終都會到達1。

陶哲軒：如果你繪制這些序列，它們看起來像布朗運動、像股票市場。它們似乎以看似隨機的模式上下波動。事實上通常就是這樣，如果你輸入一個隨機數(shù)，實際上可以證明，至少在最初，它看起來像隨機游走。而這是一個向下漂移的隨機游走。就像如果你總是在賭場玩輪盤賭，而賭注稍微對你不利。所以有時你贏，有時你輸，但在長期來看，你輸?shù)谋融A的多。通常如果你一遍又一遍地玩，你的錢包會變成零。

我證明的結(jié)果大致是，從統(tǒng)計上看，大約99%的輸入會漂移到——可能不是完全到1——但會比開始時小得多。所以這就像我告訴你，如果你去賭場，大多數(shù)情況下，如果你玩得足夠長，你最終手里的錢會比你開始時少。這有點像我證明的結(jié)果。

Lex Fridman：你能沿著這個思路繼續(xù)證明完整的猜想嗎？

陶哲軒：嗯，問題在于我使用了概率論中的參數(shù)，并且總有這種特殊事件發(fā)生。在概率論中，我們有這個大數(shù)定律，它告訴你例如如果你在一個賭場玩一個期望值隨時間遞減的游戲，你幾乎可以肯定以接近100%的概率會輸錢，但總會有一些例外情況。從數(shù)學(xué)上講，即使游戲的概率并不有利，你也可能只是稍微比輸?shù)拇螖?shù)多贏幾次。

這和Navier-Stokes方程非常相似，大多數(shù)時候你的波可以分散，但可能存在一個例外性的初始條件選擇，會導(dǎo)致你“爆炸”。而且可能存在一個例外性的特殊數(shù)字選擇，它們被放入其中會飛向無窮大，而所有其他數(shù)字會墜入地球，墜入一個點。

事實上，有一些數(shù)學(xué)家，比如Alex Kontorovich提出，這些坍縮迭代實際上類似于細胞自動機。實際上，如果你看它們在二進制中的表現(xiàn)，它們確實有點像生命游戲類型的模式。類比于生命游戲如何創(chuàng)造出巨大的自我復(fù)制物體等等，或許你可以創(chuàng)造出某種比空氣重的飛行器。一個編碼這種機器的數(shù)字，它的任務(wù)就是編碼，創(chuàng)造出某種更大的版本。

Conway也研究了這個問題，實際上非常相似，那對Navier-Stokes項目更具有啟發(fā)性。Conway研究了克拉茲問題的推廣，其中不是乘以三加一或除以二，而是有更復(fù)雜的分支列表，而不是兩種情況。也許有17種上下波動的情況，他展示了一旦你的迭代變得足夠復(fù)雜，你實際上可以編碼圖靈機，并且可以讓這些問題變得不可判定。事實上，他發(fā)明了一種編程語言，用于這類分式線性變換，他稱之為FractRat。這是一個關(guān)于“Fortran”的文字游戲。你也可以進行編程，如果你輸入的數(shù)字被編碼為素數(shù)，它就會降為零，否則就會上升，諸如此類。這類問題的總體復(fù)雜性實際上與所有數(shù)學(xué)一樣復(fù)雜。

Lex Fridman：我們之前討論過的細胞自動機的一些神秘之處，有一個數(shù)學(xué)框架來談?wù)摷毎詣訖C，也許在克拉茲猜想中也需要同類型的框架。

陶哲軒：如果你要做——不是統(tǒng)計上，而是你真的想要去做——地球上所有輸入的100%，可行的可能是統(tǒng)計學(xué)上的99%，趨近于1。但就像所有事情一樣，那看起來很難。

找到P=NP的算法，可以同時解決很多其他問題

Q：在所有著名的問題中，你覺得哪個在可觸及范圍內(nèi)是最難的問題？是黎曼猜想嗎？

陶哲軒：黎曼就在那里。P =NP是個好問題，因為它是個元問題（meta problem）。如果你解決了這個問題，從積極的意義上來說，找到了P等于NP的算法，那么這有可能同時解決很多其他問題。

Lex Fridman：我們應(yīng)該提到一些我們一直在談?wù)摰牟孪耄F(xiàn)在很多內(nèi)容都是建立在它們之上的。P=NP的連鎖反應(yīng)比其他任何的都多。

陶哲軒：如果黎曼猜想被證偽，那將給數(shù)論學(xué)家?guī)砭薮蟮木駴_擊，但它也會對密碼學(xué)產(chǎn)生連鎖效應(yīng)，因為很多密碼學(xué)都使用數(shù)論，使用涉及質(zhì)數(shù)等的數(shù)論構(gòu)造。它非常依賴于數(shù)論學(xué)家多年來積累的直覺，其中涉及質(zhì)數(shù)的運算哪些是隨機的，哪些不是。特別是，加密方法被設(shè)計成將文本信息轉(zhuǎn)換成看似隨機噪聲的文本，因此我們相信，至少在數(shù)學(xué)上，幾乎不可能被破解。但如果某個東西動搖了我們的信念，就像黎曼猜想是錯誤的，這意味著存在我們尚未知曉的質(zhì)數(shù)實際模式。有一種就會有更多，我們的許多密碼系統(tǒng)都會因此受到質(zhì)疑。

Lex Fridman：但那樣的話，你又如何去談?wù)撡|(zhì)數(shù)呢？又走向克拉茲猜想了，你希望它是隨機的對嗎？

陶哲軒：是的，所以更廣泛地說，我只是在尋找更多工具、更多方法來證明事物是隨機的。如何證明陰謀沒有發(fā)生？

Q：在你看來，P=NP這種事情是可能發(fā)生的嗎？你能想象一個它發(fā)生的宇宙嗎？

陶哲軒：這是可能的。我的意思是，存在各種情況。有一種情況是它在技術(shù)可行的，但實際上不可實施。證據(jù)有點傾向于否定，即P可能不等于NP 。

Lex Fridman：我的意思是，這看起來像是類似于黎曼猜想的那種情況。我認為證據(jù)非常傾向于否定。

陶哲軒：是這樣，傾向于否定遠比傾向于肯定要多。關(guān)于P=NP的有趣之處正在于，我們面臨的障礙也比幾乎所有其他問題都要多。所以雖然有一些證據(jù)，但我們也有很多結(jié)果排除了許多種解題方法。這是計算機科學(xué)實際上做得非常出色的一件事：它確實表明某些方法行不通。

突然，人們開始想要知道你的意見

Lex Fridman：我讀過一個有趣的故事，說當你獲得菲爾茲獎時，有個人從互聯(lián)網(wǎng)上給你寫信，問你在獲得這個崇高獎項后打算做什么？然后你很快就非常謙遜地回答說，閃亮的金屬并不能解決我目前正在研究的問題，所以我會繼續(xù)研究它們。

首先，我覺得你在那種情況下回復(fù)郵件很有趣，其次，這也顯示了你的謙遜。但無論如何，也許你可以談?wù)劮茽柶潽劊@也是我詢問Gregorio Perlman的另一種方式。你認為他為什么會以拒絕菲爾茲獎和隨之而來的價值 100 萬美元的千禧年獎而聞名？他聲稱：“我對金錢或名聲不感興趣。這個獎項對我完全無關(guān)緊要。如果證明是正確的，那么其他任何認可都不需要。”

陶哲軒：Perlman甚至在那些傾向于有些理想主義觀點的數(shù)學(xué)家中也算是個異類。我從未見過他，我想有一天見到他會很有意思，但我從未有過這個機會。我認識見過他的人：他總是對某些事情持有強烈的觀點。我的意思是，他并不是完全脫離數(shù)學(xué)界，他會發(fā)表演講、寫論文等等，但在某個時刻他決定不再和社區(qū)的其他人打交道了。

他有些失望或是什么，我不知道，他決定離開，去圣彼得堡采蘑菇或是別的什么。那也可以，你可以那樣做。那是事情的另外一面。我們解決的很多問題中，有些確實能夠?qū)嶋H應(yīng)用，那很棒。但如果你停止思考某個問題……所以他自那以后在這個領(lǐng)域沒有再發(fā)表過論文，但這沒關(guān)系，還有許多、許多其他人也這樣做了。

所以我想，我最初沒有意識到菲爾茲獎有點讓你成為體制的一部分。大多數(shù)數(shù)學(xué)家，職業(yè)數(shù)學(xué)家，只是專注于發(fā)表下一篇論文，也許提升一個等級，開始幾個項目，可能帶了一些學(xué)生之類。但突然人們開始想要知道你的意見，你必須稍微思考一下那些你可能會愚蠢地說出來的話，在過去沒有人會聽你的，現(xiàn)在這更重要。

Q：菲爾茲獎對你有束縛感嗎？你還能像以前一樣享受樂趣、保持叛逆精神、嘗試瘋狂的事情、玩弄想法嗎？

陶哲軒：我現(xiàn)在的空閑比以前少了很多，這主要是我的選擇。我的意思是，我總可以選擇拒絕，所以我拒絕了很多事情。我還可以拒絕得更多，或許我的聲譽會變得不那么可靠，以至于人們不再向我詢問。這總是一個選擇。

但我作為博士后，并沒有像我現(xiàn)在這樣花那么多時間只專注于一個問題，或者瞎搞。我仍然會做一點。但是，隨著你在職業(yè)生涯中不斷進步，軟技能（soft skills）變得越來越重要，數(shù)學(xué)在某種程度上把所有技術(shù)技能都提前到職業(yè)生涯的早期階段。所以作為博士后，你要么發(fā)表成果，要么被淘汰。你被激勵于基本上專注去證明非常技術(shù)性的定理，這樣既能證明自己，也能證明算法，但是，當你職位更高時，你必須開始指導(dǎo)學(xué)生、面試，并試圖塑造領(lǐng)域的研究方向，有時你還得處理各種行政事務(wù)。這是一種適當?shù)纳鐣跫s，因為你需要深入工作，看看什么能幫助數(shù)學(xué)家。

Lex Fridman：另一方面，建立秩序的真正積極之處在于，你可以成為照亮許多年輕數(shù)學(xué)家或?qū)?shù)學(xué)感興趣的年輕人的光。我可能會說，我挺喜歡菲爾茲獎的，它在某種程度上激勵了很多年輕人，這就是人類大腦的運作方式。同時我也想向Perlman這樣的批評獎項的人表示敬意，在他看來，那是他的原則，任何能夠按照自己的原則行事、做到大多數(shù)人都做不到的事情的人，看到這一點都令人贊嘆。

陶哲軒： 一定程度的認可是有必要的，也很重要，但同樣重要的是不要讓這些事情主宰你的生活，只關(guān)注獲得下一個大獎之類的。所以你會再次看到這些試圖只解決重大數(shù)學(xué)問題，而不去處理那些不那么“吸引人”，但確實有趣且富有啟發(fā)性的事情的人。

正如你所說的，就像人類思維的工作方式一樣，當我們理解的事物與人類相關(guān)聯(lián)，并且與少數(shù)人類相關(guān)聯(lián)時，我們會更好地理解。以我們?nèi)祟愃季S的構(gòu)造方式，我們能理解 10 到 20 個人之間的關(guān)系，但一旦超過 100 個人——我想有一個專有名稱來描述這種限制，超過這個限制，它就變成了“盲眾”。所以我們必須簡化整個群體，你知道，99.99%的人類都變成了“盲眾”，這些模型往往是不正確的，這會導(dǎo)致各種問題。

所以是的，為了讓一個學(xué)科更人性化，如果你識別出少數(shù)幾個人，并說這些人代表了這個學(xué)科，比如榜樣，這確實有一定的作用。但它也可能有害，因為我會第一個說，我自己的職業(yè)道路并不是典型的數(shù)學(xué)家的道路。

那種非常加速的教育，我錯過了很多課，我認為我一直有非常幸運的指導(dǎo)機會，我處在正確的時間、正確的地點。某人的軌跡和我不同并不意味著他們不能成為優(yōu)秀的數(shù)學(xué)家，他們會成為，但風格會非常不同，而且我們需要不同風格的人。

有時人們過于關(guān)注完成數(shù)學(xué)或其他領(lǐng)域耗時數(shù)百年或數(shù)十年的項目中的最后一步，而忽略了這一過程建立在大量先前工作之上。但如果你不是專家，很難講述這個故事。簡單地說某個人做了某件事要容易得多，歷史也因此變得簡單很多。

Lex Fridman：我認為總的來說，這是一件非常積極的事情。談到喬布斯，作為蘋果的代表，大家都知道——那令人難以置信的設(shè)計、令人難以置信的工程團隊、團隊中的那些個人。他們不是團隊，而是團隊中的個人，那個團隊有很多才華，但這只是一個簡潔的說法，就像喬布斯。

陶哲軒：是的，作為一個起點，作為一個初步的近似。

Lex Fridman：然后讀一些傳記，去了解更深的初步近似。

我們需要那些有毅力和無畏精神的人

Q：你提到你也在普林斯頓大學(xué)。當時Andrew Wiles也在那里當教授，他宣布證明了費馬大定理。現(xiàn)在回過頭來看，有了更多關(guān)于那個數(shù)學(xué)歷史時刻的背景，你當時是怎么想的？

陶哲軒：嗯，當時我是研究生。我依稀記得當時有媒體報道，我們的信箱都在同一個郵件室，突然Andrew Wiles的信箱里塞滿了信件。

我們都在茶話會上討論過，但我們不明白。我們大多數(shù)人基本上沒理解那個證明，我們理解的是高層細節(jié)。事實上，Kevin Buzzard有一個正在進行的項目要在 Lean 中形式化它。

Lex Fridman：我們能稍微偏離一下主題嗎？那有多難？因為據(jù)我所知，費馬大定理的證明涉及非常復(fù)雜的東西。

陶哲軒：是的，現(xiàn)在要將其形式化真的很難。他們使用的對象是可以定義的，他們已經(jīng)在 Lean 中定義過了，所以定義是可以做到的。這確實不是件簡單的事，但它已經(jīng)完成了。但是關(guān)于這些對象還有很多非常基本的事實，在所有這些不同的數(shù)學(xué)論文中花了數(shù)十年時間才得以證明，所有這些都需要形式化。

Kevin Buzzard有一個為期五年的資助來形式化費馬大定理，他的目標是他認為自己可能無法一直追溯到基本公理，但他希望形式化到只需要依賴黑盒，即當時一些理論家在 1980 年就已經(jīng)知道的東西，然后其他人或其他工作可以從那里繼續(xù)進行。

這與我所熟悉的數(shù)學(xué)領(lǐng)域不同。在我研究的分析學(xué)中，我們研究的對象更貼近基礎(chǔ)。我研究像素數(shù)、函數(shù)等至少在高中數(shù)學(xué)教育范圍內(nèi)可以定義的東西。但隨后，數(shù)論中存在一個非常高級的代數(shù)分支，人們已經(jīng)在這個領(lǐng)域構(gòu)建了結(jié)構(gòu)，而且是一個非常穩(wěn)固的結(jié)構(gòu)。至少在基礎(chǔ)層面，它已經(jīng)非常成熟，有相應(yīng)的教科書等等。

但確實存在這樣的情況：如果你沒有經(jīng)過這些年的學(xué)習，而想了解這個結(jié)構(gòu)的第六層在發(fā)生什么，你必須花費大量時間，他們才能讓你達到能夠看到你所熟悉的東西的程度。

Lex Fridman：關(guān)于Andrew Wiles的經(jīng)歷，有哪些方面讓你感到啟發(fā)，正如我們之前談?wù)摰模吣甑拇蟛糠謺r間都是秘密工作？

陶哲軒：這多少符合人們對數(shù)學(xué)家浪漫化的想象，在人們把數(shù)學(xué)家都想象成這些有點古怪的法師之類的人物時，這確實加強了這種觀點。他做出了偉大的成就，而且他解決問題的風格與我自己的風格非常不同，這很棒。我們需要這樣的人。

Lex Fridman：你能談?wù)勥@個么？比如在合作方面？

陶哲軒：如果一個問題太難，我就喜歡放棄，但我們需要那些有毅力和無畏精神的人。我曾與這樣的人合作，我想放棄，因為我們嘗試的第一個方法沒有成功，第二個也沒有成功。但他們堅信，并且有第三、第四和第五個方法，最終成功了。而我不得不承認，“好吧，我原本認為這不會成功，但沒錯，你一直是對的。”

人類并非天生就擁有數(shù)學(xué)中心

Q：對于那些不了解情況的人來說，你不僅因工作的卓越而聞名，還因驚人的生產(chǎn)力而著稱。所以，能不能談?wù)勀阍诓煌I(lǐng)域之間轉(zhuǎn)換的獨到之處？

陶哲軒：在不同領(lǐng)域之間轉(zhuǎn)換對我是很有效的，但也有一些人非常高效，他們能專注深入。

我認為每個人都需要找到自己的工作流程。數(shù)學(xué)中令人遺憾的一點是，數(shù)學(xué)在教學(xué)方法上似乎有一種適合所有人的方式，有一套特定的課程等等。如果你參加數(shù)學(xué)競賽或類似的活動，你也許會獲得略有不同的體驗。

但我認為許多人，他們直到很晚，甚至通常是太晚，才找到自己的數(shù)學(xué)母語。所以他們會放棄數(shù)學(xué)，并且對試圖用他們不喜歡的方式教他們數(shù)學(xué)的老師有不好的體驗。

我的理論是，人類并非天生就擁有數(shù)學(xué)中心，進化并沒有直接賦予我們大腦的數(shù)學(xué)中心。我們擁有視覺中心、語言中心以及其他一些進化中完善了的功能中心，但我們并沒有天生的數(shù)學(xué)直覺。

然而我們的其他中心足夠復(fù)雜，使我們能夠?qū)⒋竽X的其他區(qū)域用于數(shù)學(xué)活動。因此，有些人已經(jīng)掌握了如何利用視覺中心進行數(shù)學(xué)思考，在數(shù)學(xué)思考時會非常依賴視覺；有些人則改造了他們的語言中心，以非常符號化的方式思考；還有些人，如果他們非常具有競爭性并且喜歡玩游戲，大腦中有一部分非常擅長解決謎題和游戲，這部分也可以被改造用于數(shù)學(xué)。

但是當我和其他數(shù)學(xué)家談?wù)摃r，他們并不完全這樣認為，我能看出他們使用的是其他不同的思維方式，這些方式并非相互排斥，但他們可能更偏愛視覺化。我其實并不那么偏愛視覺化，我自己也需要很多視覺輔助工具。但數(shù)學(xué)提供了一個通用語言，所以即使我們思考的方式不同，我們?nèi)匀荒軌蛳嗷ソ涣鳌?/p>

Q：你能看出思考過程中使用的是不同的系統(tǒng)嗎？

陶哲軒：是的，人們走不同的路徑。他們在我感到困難的事情上非常迅速，反之，但我們?nèi)匀荒苓_到同一個目標。

但我們的教育方式——除非你有個性化的導(dǎo)師或類似的東西——教育作為某種金融技能必須大規(guī)模生產(chǎn)。你必須用同一種方式教 30 個孩子，哪怕他們有 30 種不同的風格，你不能用 30 種不同的方式來教。

對年輕人的建議

Q：對于那些在數(shù)學(xué)上苦苦掙扎，但對數(shù)學(xué)感興趣并希望變得更好的年輕學(xué)生，你對他們有什么建議嗎？

陶哲軒：這是一個棘手的問題。好消息是，現(xiàn)在課堂之外有很多豐富的數(shù)學(xué)拓展資源。在我那個年代，就已經(jīng)有數(shù)學(xué)競賽，圖書館里也有通俗數(shù)學(xué)讀物。現(xiàn)在還有YouTube、一些專門解決數(shù)學(xué)難題的論壇。

數(shù)學(xué)也出現(xiàn)在其它地方，例如一些撲克牌愛好者會對具體的概率問題感興趣，實際上在撲克、國際象棋和棒球領(lǐng)域，都有一群業(yè)余概率論愛好者群體。

數(shù)學(xué)無處不在，我希望通過Lean這類新工具，可以將更廣泛的公眾納入數(shù)學(xué)研究項目，當然目前還沒有發(fā)生。

在科學(xué)領(lǐng)域，公民科學(xué)也有一定的空間，比如天文學(xué)中有業(yè)余愛好者發(fā)現(xiàn)了彗星、生物學(xué)中有人能識別蝴蝶。在數(shù)學(xué)方面，業(yè)余數(shù)學(xué)家也可以發(fā)現(xiàn)新素數(shù)。

但在以前，我們必須驗證每一個貢獻，就像大多數(shù)數(shù)學(xué)研究項目那樣，來自公眾的意見其實幫助不大，甚至事實上，那只會耗費時間，因為光是查錯就很麻煩。

但現(xiàn)在形式化項目的好處是，它們正在聚集、吸納更多人參與其中。所以我敢肯定，有些高中生已經(jīng)為其中一些形式化項目做出了貢獻，現(xiàn)在你不需要成為博士，就可以研究原子問題。

而編程則更容易進入，你可以執(zhí)行代碼并得到結(jié)果，很快就能打印出“Hello World”。如果把編程當作一門完全理論的學(xué)科來教，你只學(xué)計算機科學(xué)、函數(shù)理論、例程等，除了專門的家庭作業(yè)以外，你實際上不會在周末為了好玩而去編程，它們會被認為和數(shù)學(xué)一樣難。

所以正如我所說，有一些非數(shù)學(xué)家群體，他們?yōu)榱四承┨囟康亩\用數(shù)學(xué)，例如優(yōu)化他們的撲克游戲策略，對他們而言，數(shù)學(xué)就變得有趣了。

Q：你對年輕人整體上有什么建議，例如如何選擇職業(yè)、找到自我和擅長的東西？

陶哲軒：我認為你需要適應(yīng)和靈活，獲得可轉(zhuǎn)移的技能，比如學(xué)習一種特定的編程語言或一門特定的數(shù)學(xué)學(xué)科或其它東西。其實這本身并不是完全可遷移，但可以從中知道如何用抽象概念進行推理，或者在出現(xiàn)問題時如何解決問題。這些都是我認為，即使在我們能使用的工具越來越好的情況下，即使你在AI支持下工作，我們?nèi)匀恍枰莆盏臇|西。

而我一直對數(shù)學(xué)的新方法感興趣，因為我認為我們現(xiàn)在很多做事的方式都是低效的。我的很多同事，都花費了很多時間在做非常常規(guī)的計算上，或者是其他科學(xué)家知道怎么做但我們不知道的事情，為什么我們不能直接搜索并快速得到回應(yīng)呢？這就是為什么我一直對探索新的工作流程很感興趣。

大約四五年前，我在一個委員會里，我們需要為數(shù)學(xué)研究所征集一些舉辦有趣研討會的想法。當時，Peter Scholze剛剛確立了他的一項新定理，計算機輔助證明方面也有一些其它的進展，看起來相當有趣。

我說，我們應(yīng)該為此舉辦一個研討會，這會是一個好主意。然后因為我對這個想法過于熱情，我被要求去實踐它。我和Kevin Buzzard、Jordan Ellenberg以及其他一些人一起做了，這是一次相當成功的研討會。我們把一群數(shù)學(xué)家、計算機科學(xué)家和其他人聚集在一起，了解了最新的進展和狀態(tài)。

這些進展非常有趣，但大多數(shù)科學(xué)家都不知道這些進展正在進行，還有很多很好的概念得以驗證，是對一些即將發(fā)生的事情的暗示。這些都發(fā)生在ChatGPT出現(xiàn)之前，其實那時，也有一場關(guān)于語言模型及其未來潛在能力的演講。這讓我為之感到興奮，于是我開始做報告，希望應(yīng)該有更多人開始關(guān)注這個領(lǐng)域。

而就在這個會議舉辦之后，ChatGPT出現(xiàn)了，然后突然間AI無處不在。我接受了大量關(guān)于這個主題的采訪，特別是有關(guān)AI和形式化證明輔助之間的互動。我說是的，它們應(yīng)該結(jié)合起來，這里存在完美的協(xié)同效應(yīng)。

然后在某個時刻，我意識到自己應(yīng)該身體力行，而不只是口頭說說而已。因為我既不在機器學(xué)習領(lǐng)域工作，也不在證明形式化領(lǐng)域工作，我僅僅只能靠權(quán)威發(fā)言，以知名數(shù)學(xué)家的身份讓人們相信這將改變數(shù)學(xué)，但這是有限度的，尤其是當我自己一點都沒有參與其中的時候，所以我認為我必須親自實踐來證明它。

實際上，我投入的很多事情，我都沒有事先預(yù)料我將花費多少時間在上面，只有當我深陷某一個項目中時，我才意識到，我已經(jīng)投入了太多。

如今數(shù)學(xué)如此龐大，沒有人能了解所有的現(xiàn)代數(shù)學(xué)。不可避免的我們會犯錯，但你不能僅用虛張聲勢來掩蓋錯誤，因為人們會要求看你的證明，如果沒有證明，那就是沒有。

數(shù)學(xué)要求我們保持誠實，雖然這并不萬能，但我們確實有一種傾向于承認錯誤的文化，因為我們總是被迫如此。

有史以來最偉大的數(shù)學(xué)家

Q：你認為誰是有史以來最偉大的數(shù)學(xué)家？

陶哲軒：首先，這取決于時間。如果你隨著時間的累積來看，歐幾里得是主要競爭者之一，然后在那之前是一些不知名的匿名數(shù)學(xué)家，無論是誰提出了數(shù)字的概念。

Lex Fridman：現(xiàn)在的數(shù)學(xué)家們還能感受到希爾伯特的影響嗎？

陶哲軒：是的，直接影響，20世紀發(fā)生的所有事情都直接受其影響。例如希爾伯特空間，我們有很多東西都是以他的名字命名的，光是數(shù)學(xué)的體系安排，以及某些概念的引入。其中23個問題極具影響力。

這里存在無處不在的旁觀者效應(yīng)。如果沒有人說你應(yīng)該做X，那么每個人都只是四處走動，等待別人做某事，但實際什么也沒做。

所以實際上，你必須教會數(shù)學(xué)本科生的是，你應(yīng)該總是嘗試去做一些事情。所以你會看到他們嘗試數(shù)學(xué)問題時總會陷入癱瘓，如果他們意識到某種技巧可以應(yīng)用，他們就會嘗試，但他們也看到了一些問題，標準技巧已經(jīng)明顯不適用的情況下，他們就會無從下手，不知道該做什么。

這讓我想起一句辛普森一家的名言：“我什么都沒嘗試，但我完全不知道怎么辦了。”所以，要知道下一步就是嘗試任何事情，無論多么愚蠢，甚至注定會失敗，你也會從失敗方式中得到啟發(fā)。比如失敗是因為你完全沒有考慮過這個假設(shè)，那么這個假設(shè)一定有用，這就是一個線索。

Q：您能詳細說一下之前提過的一個叫做結(jié)構(gòu)化拖延法的方法嗎？當你不想做一件事時，去想象一件比這更糟糕的事情，然后以不做更糟糕的事情來拖延，這是一個很有效的技巧。

陶哲軒：是的，對于任何事情，心理學(xué)都很重要。當你和馬拉松運動員交談時，他們談?wù)摰淖钪匾氖虑椴皇怯?xùn)練方案或飲食，而在很大程度上是心理，只要自我欺騙相信問題是可行的，這樣你就會有動力去做它。

Q：是否存在我們?nèi)祟惔竽X永遠無法理解的東西？

陶哲軒：作為數(shù)學(xué)家，根據(jù)歸納法，一定存在足夠大的數(shù)字，而我們無法理解，這是我首先能想到的。

Lex Fridman：那么集體智慧可行嗎？

陶哲軒：是的，我認為復(fù)數(shù)意義上的人類，原則上在狀態(tài)好時，擁有比單個個體總和更多的智慧。當然它也可能更少。

復(fù)數(shù)意義上的數(shù)學(xué)共同體是一個令人難以置信的超級智能體，沒有任何單個的人類數(shù)學(xué)家能與之匹敵。有時你能看到在數(shù)學(xué)社區(qū)中，對于非常困難的問題，能夠迅速給出快速的答案。作為專家，旁觀這個過程實際上是種享受。

Q：對于人類文明的整個過程，是什么讓你充滿希望？

陶哲軒：我認為年輕一代總是非常有創(chuàng)造力、熱情和發(fā)明力。和年輕學(xué)生一起工作是一種樂趣。要知道科學(xué)的進步告訴我們，過去非常困難的問題，現(xiàn)在變得非常容易解決。

比如說導(dǎo)航，了解自己在地球上的位置，這曾經(jīng)是個非常可怕的問題，人們因此喪命或者傾家蕩產(chǎn)，但現(xiàn)在我們口袋里的設(shè)備就能自動幫我們做到，這已經(jīng)不再是問題。現(xiàn)在對于我們來說，似乎不可行的事情，只有可能是家庭作業(yè)練習。

Lex Fridman：是的，所以我總是對生命的有限性感到悲哀，我們無法看到我們作為一個文明創(chuàng)造的所有酷炫事物。

陶哲軒：現(xiàn)在已經(jīng)發(fā)生了很多事情，如果能夠回到過去，和十幾歲的自己交談，或者僅僅是讓互聯(lián)網(wǎng)和現(xiàn)在的人工智能交談，它們都已經(jīng)逐漸被內(nèi)化。你會理所當然地認為AI可以聽懂我們說話，并對任何問題給出合理的或者稍微有點錯誤的答案。但這在兩年前，還是令人震驚的。

Lex Fridman：在當下看著互聯(lián)網(wǎng)上的各種反應(yīng)，這種戲劇性場面也很有趣。人們很快就把一切都視為理所當然，然后我們?nèi)祟愃坪跄苡萌魏巫约簞?chuàng)造出來的東西，自娛自樂。有人持一種觀點，另一個人需要持相反觀點，然后為此爭論不休。但是當你退后一步看待事情的軌跡時，即使是機器人技術(shù)的進步，也會感嘆人類的創(chuàng)造力。

陶哲軒：是的。當基礎(chǔ)設(shè)施和文化健康時，人類共同體可以比其中的個體更聰明、成熟和理性得多。

Lex Fridman：沒錯，在有一個地方，我總是能夠看到理性，那就是您博客的評論區(qū)，那里匯集了很多非常聰明的人。好的，最后非常感謝您抽出時間接受訪談。

陶哲軒：謝謝，這是我的榮幸。

Lex Fridman：最后請讓我引用伽利略的一句話為本次訪談收尾：

數(shù)學(xué)是上帝用來書寫宇宙的一種語言。

參考鏈接：
[1]https://lexfridman.com/terence-tao-transcript
[2]https://www.youtube.com/watch?v=HUkBz-cdB-k
[3]https://github.com/teorth/equational_theories
[4]https://arxiv.org/abs/math/0211159

—完—