陶哲軒推薦：2高中生發(fā)現(xiàn)勾股定理新證明，論文已發(fā)《美國(guó)數(shù)學(xué)月刊》

金磊 發(fā)自 凹非寺

量子位 | 公眾號(hào) QbitAI

兩個(gè)高中生發(fā)現(xiàn)的勾股定理新證明，現(xiàn)在論文來(lái)了。

而且就在剛剛，數(shù)學(xué)大神陶哲軒在看完這篇論文之后評(píng)價(jià)道：

前幾年聽(tīng)說(shuō)這個(gè)消息時(shí)候，還沒(méi)有任何實(shí)質(zhì)性的細(xì)節(jié)證明。

但現(xiàn)在，（在一些限制條件下）她們確實(shí)發(fā)現(xiàn)了至少五個(gè)新證明，而且跟任何已有的證明都不相同。

這兩位高中生分別是Ne’Kiya Jackson和Calcea Johnson。

她們?cè)?022年發(fā)現(xiàn)勾股定理新證明的時(shí)候，正就讀于美國(guó)新奧爾良的圣瑪麗學(xué)院（St. Mary’s Academy）。

勾股定理想必大家都已經(jīng)非常熟悉了，包括那句耳熟能詳?shù)?strong>“勾三股四弦五”，以及它的基本公式a2+b2=c2。

雖然這個(gè)定理已經(jīng)有2500多年的歷史，但毫不夸張地說(shuō)，它的重要性依然貫穿于現(xiàn)代數(shù)學(xué)之中。

當(dāng)時(shí)她們二人提出新證明時(shí)，可以說(shuō)是在圈內(nèi)引起了不小的轟動(dòng)。

因?yàn)殚L(zhǎng)期以來(lái)，數(shù)學(xué)家們基本上都采用代數(shù)和幾何的方法來(lái)證明這個(gè)定理。

但她們采用的卻是三角學(xué)（Trigonometry，基于對(duì)角度及邊長(zhǎng)之間關(guān)系的直接推導(dǎo)）這個(gè)數(shù)學(xué)分支來(lái)做證明。

這是特別具有挑戰(zhàn)性的一件事情。

因?yàn)槿菍W(xué)在很大程度上就是基于勾股定理，大多數(shù)情況下就會(huì)導(dǎo)致所謂的“循環(huán)論證”（circular reasoning），即證明過(guò)程中偷用了待證的結(jié)果。

早在1927年，數(shù)學(xué)家Elisha Loomis就曾斷言道：

使用三角學(xué)的規(guī)則無(wú)法完成對(duì)勾股定理的證明。

然而，就是這么一個(gè)看似“不可能”的方法，卻被兩位高中生給突破了。

要知道，當(dāng)時(shí)跟她倆采用類似方法做過(guò)證明的，只有2位專業(yè)的數(shù)學(xué)家——Jason Zimba和Nuno Luzia，分別于2009年和2015年提出。

而現(xiàn)如今，二人正式在《美國(guó)數(shù)學(xué)月刊》公布了論文，把證明過(guò)程的細(xì)節(jié)內(nèi)容都亮了出來(lái)，也得到了陶哲軒的認(rèn)可。

更重要的是，這篇論文不僅詳細(xì)介紹了五種全新的證明方法，她們還提出了一個(gè)系統(tǒng)性的方法，預(yù)計(jì)能夠生成至少五種額外的新證明。

換言之，五個(gè)新證明是保底的，也可以達(dá)到十個(gè)！

其中，只有一個(gè)證明是她們?cè)?023年3月參加學(xué)術(shù)會(huì)議時(shí)展示過(guò)的，另外九個(gè)是全新的。

那么她們二人到底是如何做到，我們繼續(xù)往下看。

三角學(xué)證明和三個(gè)先決條件

首先，我們來(lái)了解她們二人對(duì)三角學(xué)證明的解釋。

三角學(xué)證明是使用三角函數(shù)的性質(zhì)、恒等式和基本定理來(lái)證明幾何或代數(shù)命題的方法。

它通常利用三角函數(shù)（如正弦、余弦、正切等）之間的關(guān)系，結(jié)合已知的三角恒等式和公式來(lái)得出結(jié)論。

實(shí)際上，正弦和余弦的三角比率是為一個(gè)銳角α定義的，通過(guò)創(chuàng)建一個(gè)直角三角形ABC，其中α是兩個(gè)銳角之一，然后比較三條邊中的兩條的長(zhǎng)度：

sinα定義為對(duì)邊BC與斜邊AB的比值，cosα是鄰邊AC與斜邊的比值。

但是，通過(guò)測(cè)量直角三角形來(lái)定義正弦或余弦只對(duì)銳角有效，所有其他角度需要一個(gè)完全不同的方法。

對(duì)于這些角度，她們使用單位圓：

從點(diǎn)(1, 0)開(kāi)始，向逆時(shí)針?lè)较颍▽?duì)于負(fù)角是順時(shí)針?lè)较颍┭刂鴪A移動(dòng)，直到達(dá)到所需的中心角α，最終到達(dá)點(diǎn)(x, y)。然后我們定義cosα = x和sinα = y。

對(duì)于一個(gè)銳角，這兩種方法給出的正弦或余弦函數(shù)值是相同的，如圖1所示：

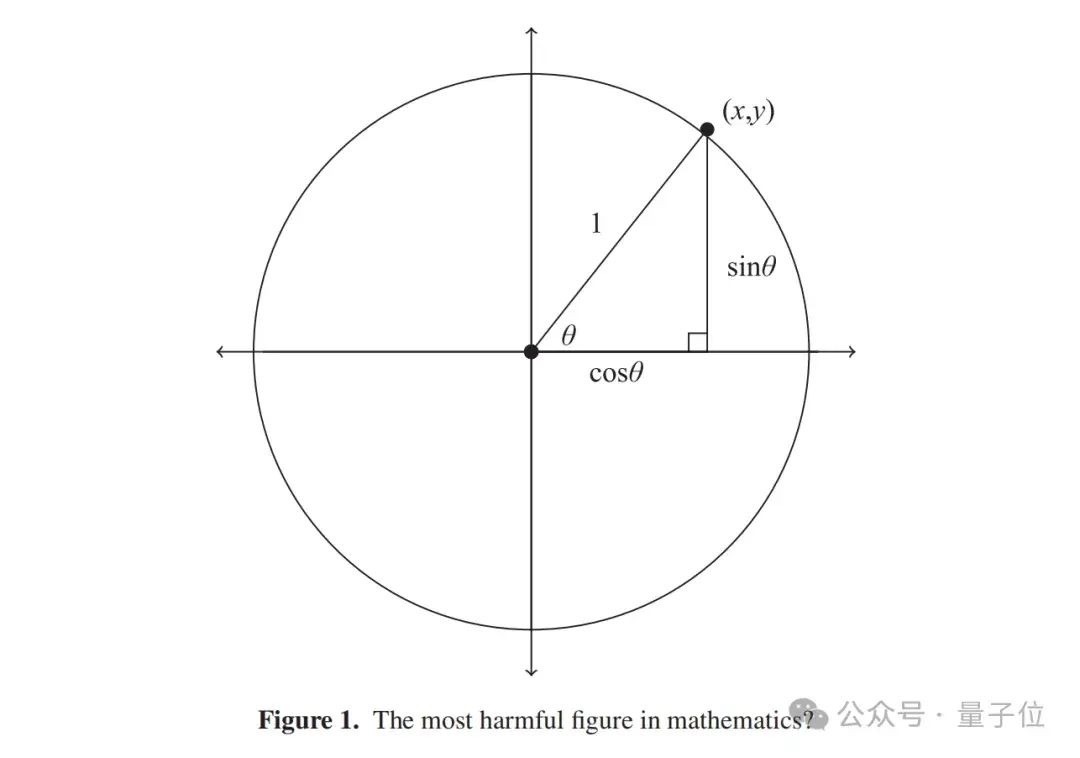
但只有第一種方法可以合理地被稱為三角學(xué)的，第二種方法可能被稱為圓的（cyclotopic）會(huì)更恰當(dāng)一些，如圖2所示：

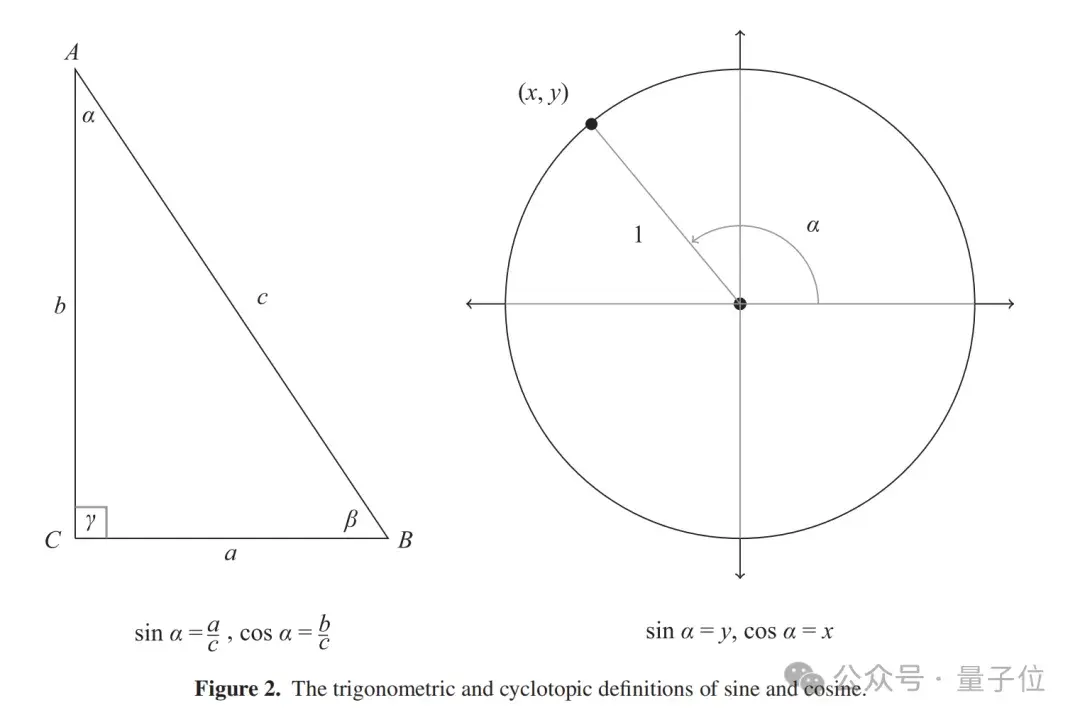
實(shí)際上，這兩種方法之間的區(qū)別意味著，通過(guò)余弦定理（我們從c2 = a2 + b2 ? 2abcosγ開(kāi)始，讓?duì)贸蔀橐粋€(gè)直角）來(lái)證明勾股定理是一個(gè)圓的證明，而不是一個(gè)三角學(xué)的：

三角學(xué)不能計(jì)算一個(gè)直角的余弦值，而圓的測(cè)量告訴我們cos(90°) = 0。

同樣，使用cos(α ? β)的公式（讓?duì)?= β在恒等式cos(α ? β) = cosαcosβ + sinα*sinβ中）來(lái)證明勾股定理也是圓的而不是三角學(xué)的，使用sin(α + β)的公式也是如此，其中α和β是互補(bǔ)角。

聲稱一個(gè)證明是三角學(xué)的也可以基于其他理由被否認(rèn)。

例如，勾股定理最著名的證明之一使用了相似性△ABC ～ △ACD ～ △CBD，如圖3所示：由于a/c = x/a和b/c = y/b，有c = x + y = a2/c + b2/c，從而得出a2 + b2 = c2。

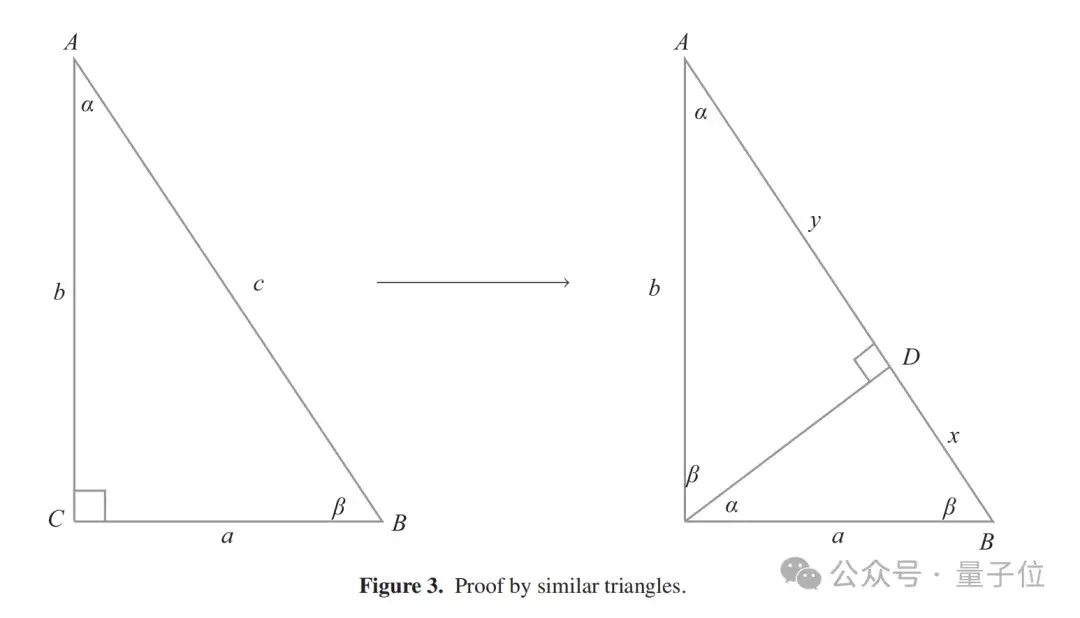
但這個(gè)證明可以很容易地被改寫(xiě)為三角學(xué)。

由于a/c = x/a = sinα，有x = asinα = (csinα)sinα = csin2α，同樣y = ccos2α。然后c = x + y = c(sin2α + cos2α)，從中得出1 = sin2α + cos2α = (a/c)2 + (b/c)2，因此a2 + b2 = c2。

但在這里使用三角學(xué)術(shù)語(yǔ)并沒(méi)有增加任何東西——事實(shí)上，它只會(huì)使相同的方法更加復(fù)雜——因此可以說(shuō)這個(gè)證明使用了相似三角形，而不是三角學(xué)。

更一般地，任何證明a2 + b2 = c2的證明都可以通過(guò)將csinα寫(xiě)作a和ccosα寫(xiě)作b（或者通過(guò)重新縮放邊a、b和c到sinα、cosα和1）來(lái)改寫(xiě)為“三角”證明。

首先證明sin2α + cos2α = 1，之后反向替換sinα = a/c和cosα = b/c以顯示a2 + b2 = c2。

這種幻覺(jué)顯示需要對(duì)一個(gè)“三角”勾股定理的證明持懷疑態(tài)度，這種證明以這種迂回的方式工作（即，首先證明恒等式sin2α + cos2α = 1）以確保“三角學(xué)”不僅僅是使用正弦和余弦術(shù)語(yǔ)對(duì)邊長(zhǎng)的不必要重述。

為了確保證明勾股定理的過(guò)程不依賴于循環(huán)論證，她們二人在論文中提到了三個(gè)先決條件（preliminaries）：

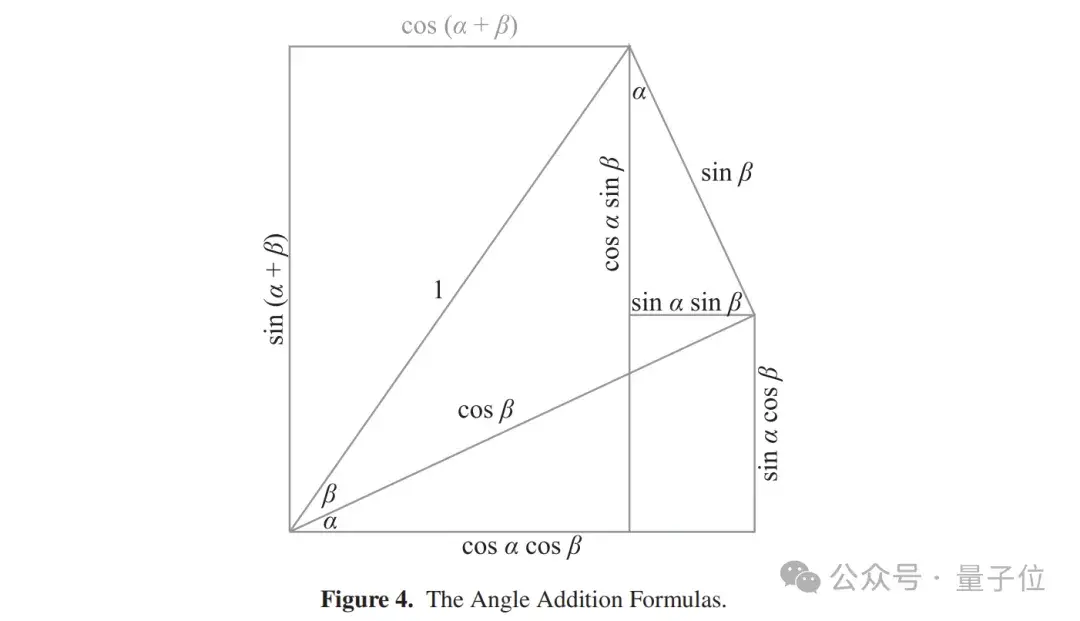
• 角度加法公式：

角度加法公式主要用于三角函數(shù)中的正弦和余弦運(yùn)算。

對(duì)于銳角α、β 和 α+β，正弦和余弦滿足以下關(guān)系：

sin(α+β)=sinαcosβ+cosαsinβ
cos(α+β)=cosαcosβ?sinαsinβ

這些公式可以確保在不依賴勾股定理的情況下，能夠?qū)φ液陀嘞疫M(jìn)行直接計(jì)算，從而保持證明的嚴(yán)謹(jǐn)性和獨(dú)立性。

• 正弦定理

正弦定理被用于分析某些三角形中邊長(zhǎng)之間的關(guān)系。

正弦定理的核心是描述了三角形各邊的比例關(guān)系，當(dāng)已知兩個(gè)角和它們的對(duì)邊時(shí)，可以確定第三邊的長(zhǎng)度。正弦定理表述如下：

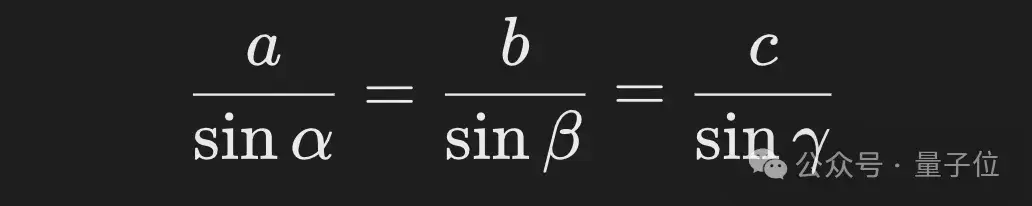
這些公式用于接下來(lái)的證明中的多個(gè)步驟，特別是用于連接和計(jì)算不同邊長(zhǎng)，以便在已知特定角度的情況下得出邊長(zhǎng)關(guān)系。

• 等腰直角三角形的特殊情況

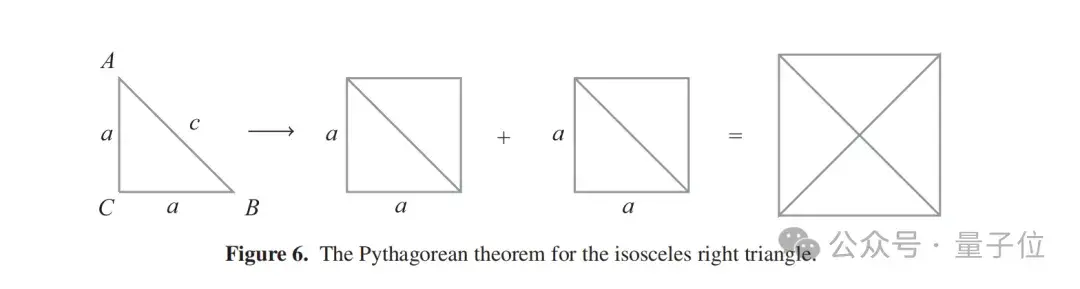
等腰直角三角形中，兩個(gè)直角邊相等，這種對(duì)稱性簡(jiǎn)化了許多計(jì)算。這種特殊三角形的邊長(zhǎng)關(guān)系，直接得出邊長(zhǎng)滿足勾股定理：

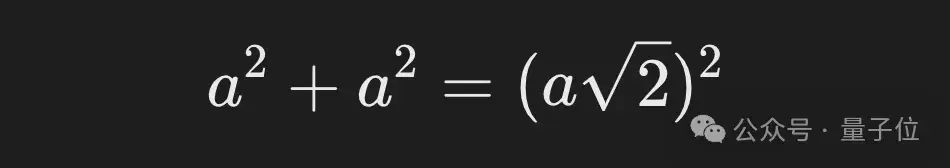
因此，對(duì)于等腰直角三角形，證明過(guò)程變得更加簡(jiǎn)潔，因?yàn)閮蛇叺钠椒胶椭苯拥扔谛边叺钠椒健?/p>

接下來(lái)，就到了關(guān)鍵的證明部分。

五至十個(gè)勾股定理新證明

為了便于閱讀和理解，這部分我們將直接放上證明的原文內(nèi)容（公式著實(shí)不太好展示）。

第一個(gè)證明

第二個(gè)證明

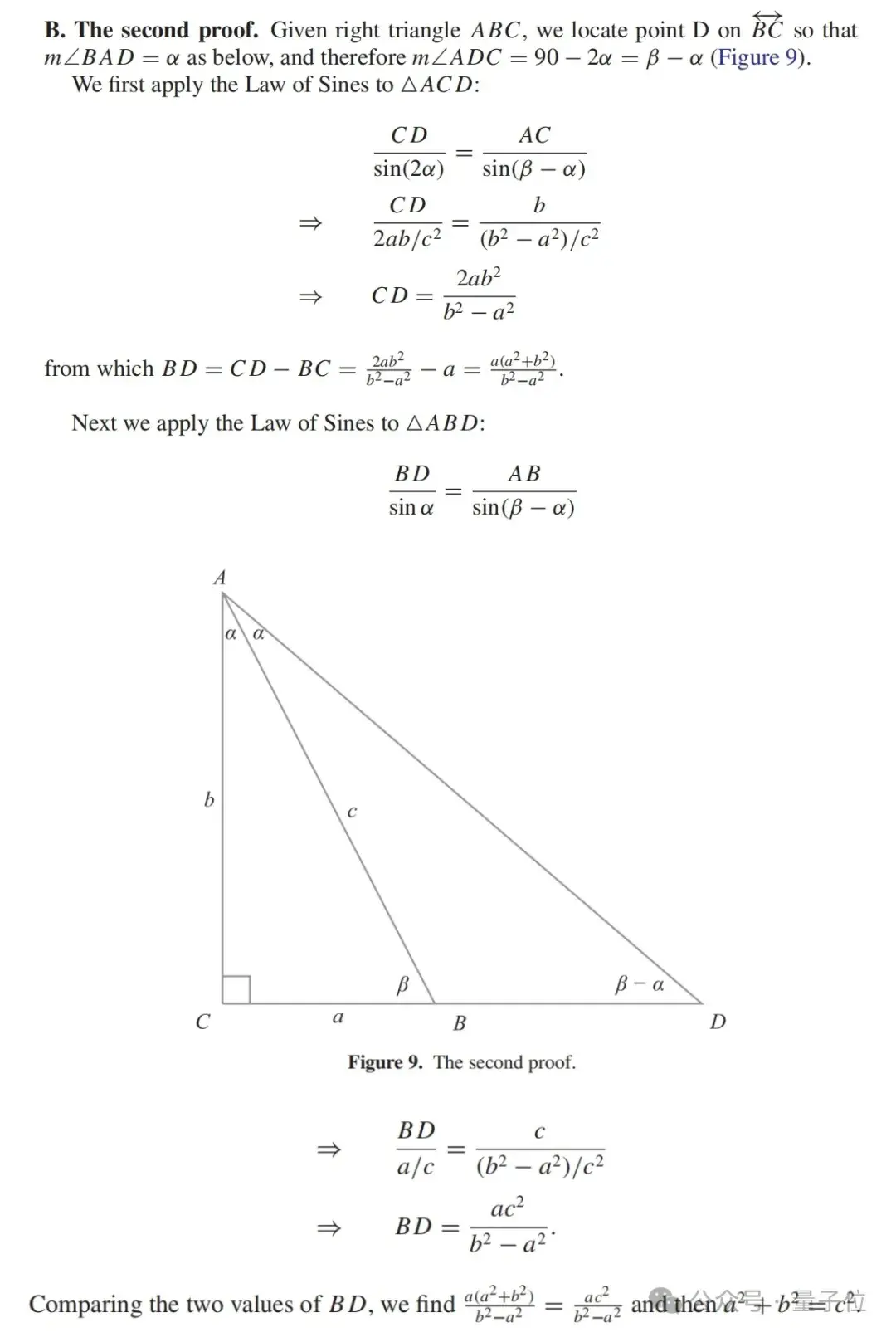
第三個(gè)證明

第四個(gè)證明

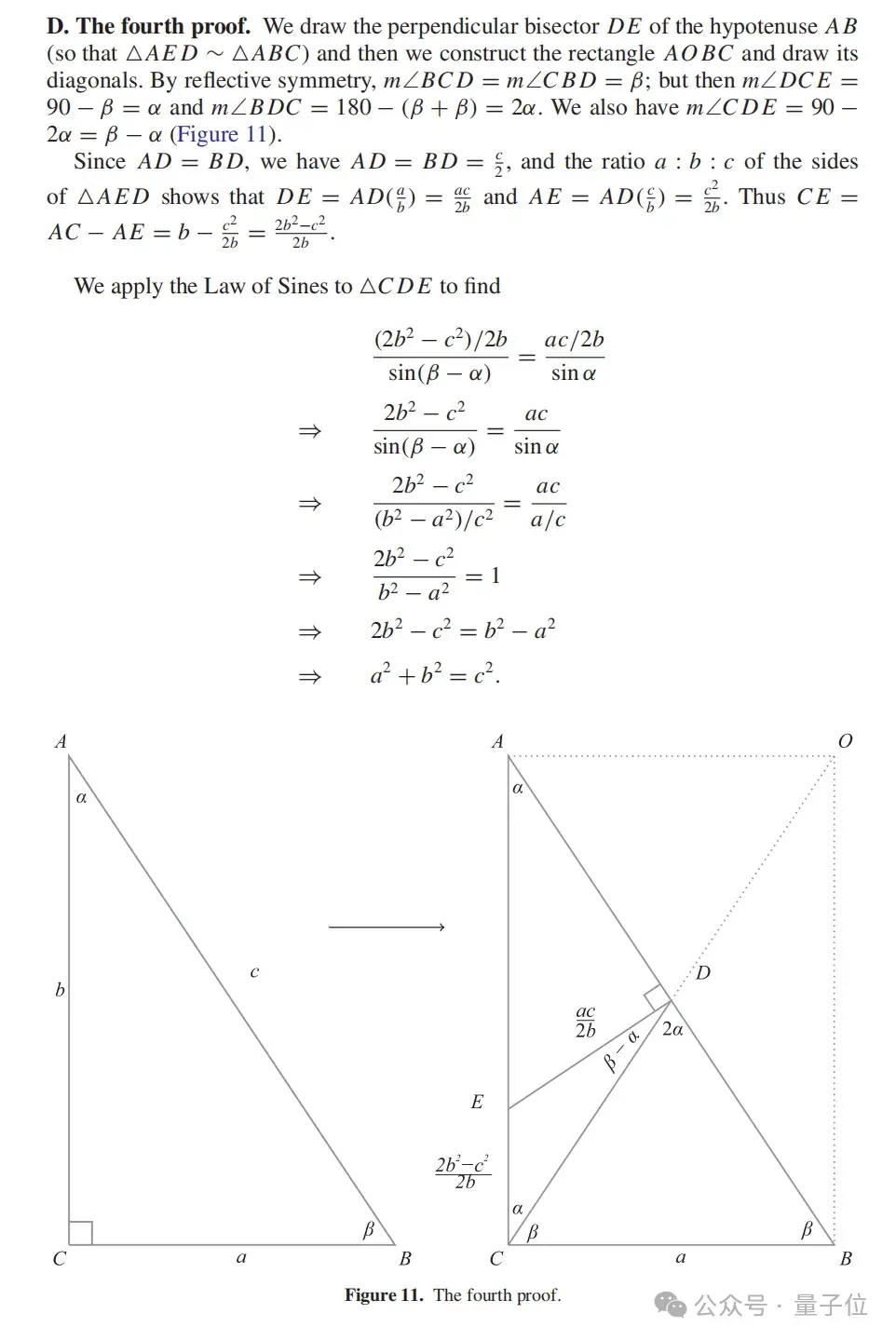
第五個(gè)證明

除此之外，論文還對(duì)具體方法做了展開(kāi)介紹。

二人先是提出了一個(gè)她們這項(xiàng)研究所要解決的基本問(wèn)題，即：

我可以用給定的直角三角形△ABC創(chuàng)造出哪些新的直角三角形？

將對(duì)新三角形的構(gòu)造限制在那些角度為△ABC的三個(gè)角度α、β和 90°（即 α+β）的整數(shù)倍之和或差的三角形上。

由此，這個(gè)問(wèn)題的答案變得直接明了。

引理1

a) 如果 △ABC是一個(gè)等腰直角三角形（即 α=β=45°），那么所有角度為 α和 β的整數(shù)線性組合的三角形都是等腰直角三角形。

b) 如果在直角三角形 △ABC中 α<β，則存在一個(gè)直角三角形，其銳角為 2α和 β?α。此外，對(duì)于每一對(duì) {α,β}，2α和 β?α是唯一能夠形成直角三角形銳角的 α和 β的整數(shù)線性組合。

證明

a) 由于等腰三角形 △ABC的三個(gè)角度都是 45°的倍數(shù)，所以任何新三角形的所有角度（這些角度被限制為 △ABC的角度之和或差）仍然是 45°的倍數(shù)，因此我們得到的三角形必定是一個(gè)等腰直角三角形。換句話說(shuō)，如果我們從等腰直角三角形開(kāi)始，那么無(wú)法構(gòu)造出新的三角形。

b) 現(xiàn)在假設(shè) α<β。如果新構(gòu)造的直角三角形中的一個(gè)銳角為 mα+nβ（其中 m,n∈Z），則其補(bǔ)角為：

90°?(mα+nβ)=(α+β)?(mα+nβ)=(1?m)α+(1?n)β

如果整數(shù) n和 1?n都不為零，那么其中一個(gè)（假設(shè)為 n）是負(fù)數(shù)，那么將 n替換為 ∣n∣我們可以看到其中一個(gè)角度是 mα?nβ，其中 m>n>0。

但是當(dāng) α的度數(shù)為 90n/(m+n)時(shí)，其補(bǔ)角 β的度數(shù)為 90m/(m+n)，這種構(gòu)造將會(huì)產(chǎn)生一個(gè)角度 mα?nβ=m?90n/(m+n)?n?90m/(m+n)=0。

這表明我們必須有 n=0，即其中一個(gè)銳角度數(shù)是 mα的某個(gè) m∈N。

如果 m=1，那么我們簡(jiǎn)單地恢復(fù)了原始三角形 △ABC。如果 m=2，那么我們得到一個(gè)新的直角三角形，其銳角為 2α和 β?α（注意 2α<90°因?yàn)?α<45°）。

最后，我們看到 m≥3是不可能的，因?yàn)槿绻?30°≤α<45°，則不會(huì)存在這樣的三角形。

我們的引理確切地告訴我們?nèi)绾螌ふ夜垂啥ɡ淼淖C明（對(duì)于非等腰直角三角形）：從我們的原始三角形ABC開(kāi)始，我們盡可能多地嘗試創(chuàng)建一個(gè)新的直角三角形，其角度測(cè)量為2α、β ? α和90°。

例如，創(chuàng)建一個(gè)2α角度的最簡(jiǎn)單方法是結(jié)合兩個(gè)△ABC的副本，如圖13所示。

這創(chuàng)造了等腰三角形ABB’，其角度測(cè)量為2α、β和β，所以下一步是取其中一個(gè)測(cè)量為β的角度，并將其轉(zhuǎn)換為測(cè)量為β ? α或90度的角度。

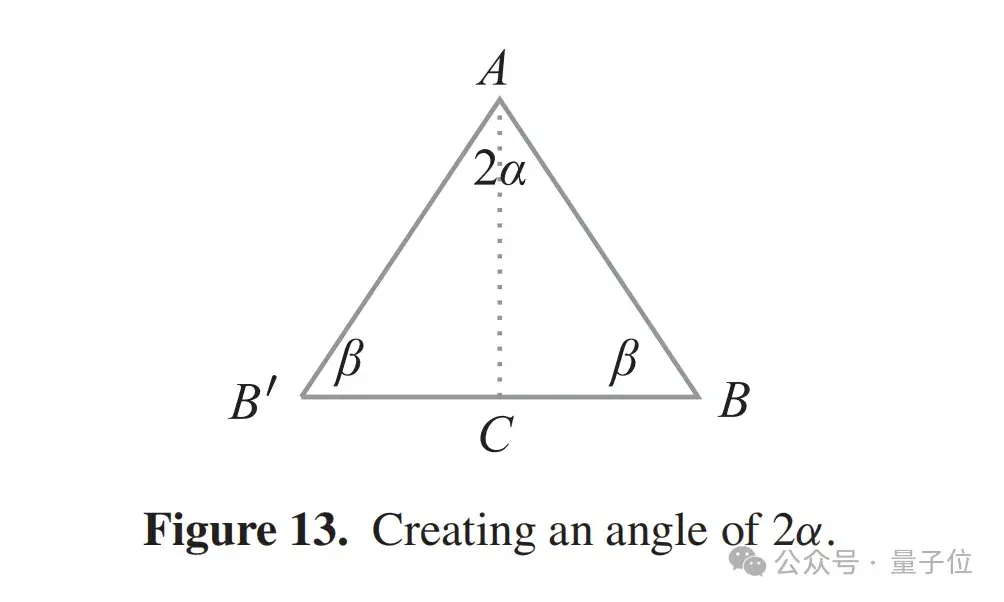
為了在頂點(diǎn)B’處創(chuàng)建一個(gè)90度的角度，我們構(gòu)建一個(gè)射線，使其與BB’成α角度。如果我們?nèi)缓笱娱L(zhǎng)邊AB以在點(diǎn)D處與射線相交，我們就得到了我們第一個(gè)證明的圖形（圖14）。

或者，如果我們?cè)谛边匒B的另一側(cè)創(chuàng)建2α角度，并延長(zhǎng)BC以在點(diǎn)D處與新射線相交，如下所示，我們得到了直接導(dǎo)致我們第二個(gè)證明的圖形（圖15）。

而至于另外五種證明方法，感興趣的讀者可以點(diǎn)擊文末鏈接查看詳情哦。

靈感來(lái)自一個(gè)高中數(shù)學(xué)競(jìng)賽

但除了這次勾股定理的新證明之外，Ne’Kiya Jackson和Calcea Johnson背后的故事也是值得聊一聊。

在這篇論文的致謝部分中，她們也對(duì)此做了講述。

事情的起因是二人當(dāng)年參加的一場(chǎng)高中數(shù)學(xué)競(jìng)賽，其中就有一道加分題：

創(chuàng)建一種新的勾股定理證明方法，獎(jiǎng)勵(lì)500美元。

于是，她們決定各自挑戰(zhàn)這道題目。

然而，這項(xiàng)任務(wù)比她們最初預(yù)想的要困難得多，二人花費(fèi)了無(wú)數(shù)個(gè)不眠之夜，反復(fù)嘗試并失敗。經(jīng)過(guò)大約一個(gè)月的努力，她們分別完成了自己的證明并提交了作業(yè)。

并且她們的數(shù)學(xué)老師Rich認(rèn)為證明的方法足夠新穎，值得在數(shù)學(xué)會(huì)議上展示。

盡管她們對(duì)自己的工作并沒(méi)有太大的信心，但還是決定嘗試一下。

接下來(lái)的兩三個(gè)月中，二人把所有空閑時(shí)間都投入到完善和打磨她們的工作中。

她們既獨(dú)立工作也共同合作，不僅在放學(xué)后，甚至周末和假期都在繼續(xù)努力。

在此過(guò)程中，在Rich的指導(dǎo)下，她們創(chuàng)造了更多的證明方法。

盡管她們不確定是否有機(jī)會(huì)在會(huì)議上展示，因?yàn)橥ǔＶ挥袑I(yè)數(shù)學(xué)家或偶爾的大學(xué)生能夠在這樣的會(huì)議上發(fā)言，但她們的高中作品最終還是受到了重視，并被批準(zhǔn)在2023年3月的美國(guó)數(shù)學(xué)學(xué)會(huì)東南分會(huì)會(huì)議上展示。

Ne’Kiya和Calcea是會(huì)議中最年輕的與會(huì)者和演講者，雖然她們感到非常緊張，但想到這是她們所有努力的結(jié)晶，也讓她們有了信心去展示。

她們的演講獲得了成功，隨后也受到了美國(guó)數(shù)學(xué)學(xué)會(huì)的鼓勵(lì)，將其研究成果提交給學(xué)術(shù)期刊。

這對(duì)二人來(lái)說(shuō)是最艱巨的任務(wù)，因?yàn)樗齻儗?duì)撰寫(xiě)學(xué)術(shù)論文毫無(wú)經(jīng)驗(yàn)。

當(dāng)時(shí)，她們還在適應(yīng)大學(xué)生活的各種挑戰(zhàn)，比如學(xué)習(xí)LaTeX代碼、完成小組的5頁(yè)論文、提交實(shí)驗(yàn)數(shù)據(jù)分析等。

但在導(dǎo)師們的指導(dǎo)下，再加上大量的個(gè)人努力，她們最終完成了論文的撰寫(xiě)。

現(xiàn)在回頭看這個(gè)過(guò)程，Ne’Kiya和Calcea在論文中這樣寫(xiě)到：

到達(dá)這一步對(duì)我們來(lái)說(shuō)并不容易，也不是一條直線前進(jìn)的道路。

我們沒(méi)有任何現(xiàn)成的路線圖，也不確定工作是否會(huì)得到認(rèn)可。很多次我們都想放棄，但最終，還是決定堅(jiān)持到底，完成已經(jīng)開(kāi)始的事情。

而對(duì)于這篇論文，陶哲軒也發(fā)表了自己的想法：

這篇論文提醒了我們，即使是數(shù)學(xué)中最古老和最成熟的基礎(chǔ)結(jié)果，有時(shí)也可以從一個(gè)全新的角度重新審視。

除此之外，目前也有不少的數(shù)學(xué)家已經(jīng)加入到了討論中：

完整論文放下面了，感興趣的小伙伴可以閱讀哦~

論文地址：https://www.tandfonline.com/doi/full/10.1080/00029890.2024.2370240#d1e4959

參考鏈接：
[1]https://mathstodon.xyz/@tao/113391326199704210
[2]https://www.sciencedaily.com/releases/2024/10/241028132143.htm